$5, 5 r, 5 r^{2}$ are sides of a triangle. Which value of r cannot be possible (a) $3 / 2$ (b) $5 / 4$ (c) $3 / 4$ (d) $7 / 4$

A

$\frac{5}{4}$

B

$\frac{7}{4}$

C

$\frac{3}{2}$

D

$\frac{3}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let $α = 5, b = 5 r and c = 5 r^{2}$ We know that, in a triangle sum of 2 sides is always greater than the traid side.
$∴ a + b > c, b + c > α and c + a > b$
Now, $a + b > c$
$∴ a + b > c, b + c > α and c + a > b$
Now, $a + b > c \Rightarrow 5 + 5 r > 5 r^{2} - 5 r - 5 < 0$
$\Rightarrow r^{2} - r - 1 < 0$
$\Rightarrow r^{2} - r - 1 < 0$
$\Rightarrow [r - (\frac{1 - \sqrt{5}}{2})] [r - (\frac{a + \sqrt{5}}{2})] < 0$
$[∵ roots of a x^{2} + b x + x = 0 are given by x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 α} and r^{2} - r 1 = 0 \Rightarrow r = \frac{1 \pm \sqrt{1 + 4}}{2} = \frac{1 \pm \sqrt{5}}{2}]$
$\Rightarrow r \in (\frac{1 - \sqrt{5}}{2}, \frac{1 + \sqrt{5}}{2}) (i)$

Similarly, $b + c > a$
$\Rightarrow 5 r + 5 r^{2} > 5$
$\Rightarrow r^{2} + r - 1 > 0$
$[r - (\frac{- 1 - \sqrt{5}}{2})] [r - (\frac{- 1 + \sqrt{5}}{2})] > 0$
$[∵ r^{2} + r - 1 = 0 \Rightarrow r = \frac{- 1 \pm \sqrt{1 + 4}}{2} = \frac{- 1 \pm \sqrt{5}}{2}]$
$\Rightarrow r \in (- \infty, \frac{- 1 - \sqrt{5}}{2}) \cup (\frac{- 1 + \sqrt{5}}{2}, \infty) (i i)$

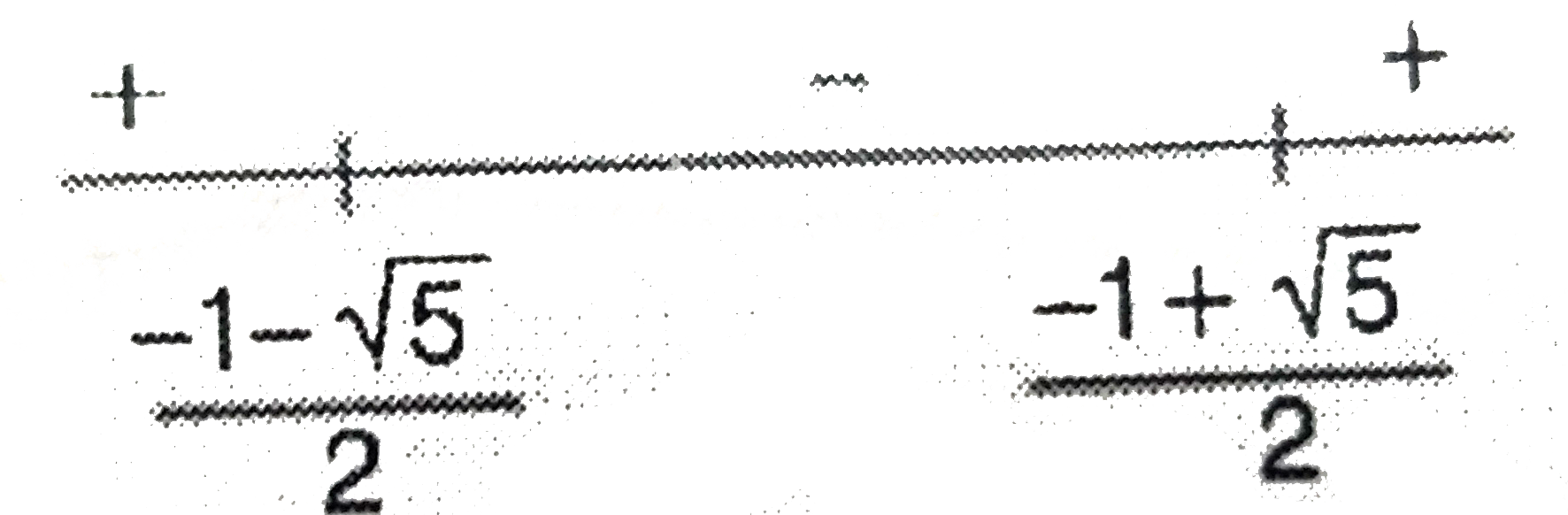
and $c + a > b$
$\Rightarrow 5 r^{2} + 5 > 5 r$
$\Rightarrow r^{2} - r + 1 > 0$
$\Rightarrow r^{2} - 2 . \frac{1}{2} r + {(\frac{1}{2})}^{2} + 1 - {(\frac{1}{2})}^{2} > 0$
$\Rightarrow {(r - \frac{1}{2})}^{2} + \frac{3}{4} > 0$
$\Rightarrow r \in R ... (i i i)$
From Eqs. (i), (ii) and (iii), we get $r \in (\frac{- 1 + \sqrt{5}}{2}, \frac{1 + \sqrt{5}}{2})$

and $\frac{7}{4}$ is the only value that does not satisfy.

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If 5, 5r and $5 r^{2}$ are the lengths of the sides of a triangle, then r cannot be equal to
A $\frac{3}{2}$
B $\frac{3}{4}$
C $\frac{5}{4}$
D $\frac{7}{4}$
If the lengths of the side of a triangle are 3,4 and 5 units, then find the circum radius R.
A $2.0$
B $2.5$
C $3.0$
D $3.5$

IIT JEE PREVIOUS YEAR-THEORY OF EQUATIONS-SOME SPECIAL FORMS

Home
Ask Doubt
Profile