Obtain the expression for electric field due to an uniformly charge spherical shell. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Electric field due to a uniformly charged shell : Consider a uniformly charged spherical shell of radius R and total charge Q . The electric field at point outside and inside the sphere is found using Gauss law .

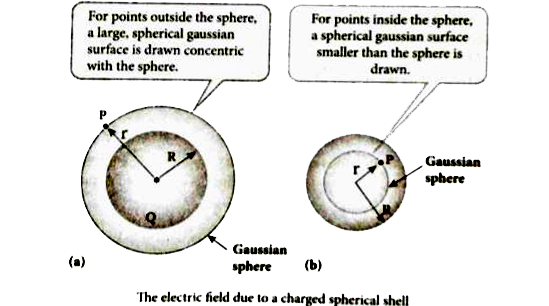
Case (a) At a point outside the shell $(r > R)$ : Let us choose a point P outside the shell at a distance r from the center as shown in figure (a) . The charge is uniformly distributed on the surface of the surface of the sphere ( spherical symmetry) . Hence the electric field must point radially outward if $Q > 0$ and point radially in ward if $Q < 0 .$ So we choose a spherical Gaussian surface of radius r and the total charge enclosed by this Gaussian surface is Q . Applying Gauss law ,
$\oint \to E . d \to A = \frac{Q}{ε_{0}}$
The electric field $\to E$ and $d \to A$ point in the same direction ( outward normal ) at all the point on the Gaussian surface . The magnitude of $\to E$ is also the same at all points due to the spherical symmetry of the charge distribution .
Hence $E \int Gaussian surface d A = \frac{Q}{ε_{0}}$
But $\int Gaussian surface$ dA = total area of Gaussian surface $= 4 π r^{2}$ . Substituting this value in equation (2).
$e .4 π r^{2} = \frac{Q}{ε_{0}}$
$E .4 π r^{2} = \frac{Q}{ε_{0}}$ (or) $E = \frac{1}{4 π ε_{0}} \frac{Q}{r^{2}}$
In vector form $\to E = \frac{1}{4 π ε_{0}} \frac{Q}{r^{2}} ˆ r$
The electric field is radially outward if $Q > 0$ and radially inward if $Q < 0$ . From equation (3) we infer that the electric field at a point outside the shell will be same as if the entire charge Q is concentrated at the centre of the spherical shell . (A similar result is observed in gravitation for gravitational force due to a spherical shell with mass M )
Case (b) : At a point on the surface of the spherical shell (r=R) : The electrical fiedl at points on the spherical shell ( r= R) is given by
$\to E = \frac{Q}{4 π ε_{0} R^{2}} ˆ r$
Case (c ) At a point inside the spherical shell $(r < R)$ : Consider a point P inside the shell at a distance r from the center . A Gaussian sphere of radius r is constructed as shown in teh figure (b) Applying law
$\int Gaussian furface \to E . d \to A = \frac{Q}{ε_{0}}$
$E .4 π r^{2} = \frac{Q}{ε_{0}}$
Since Gaussian surface encloses no charge So Q = 0 . The equation ( 5) becomes
E=0 $(r < R)$
The electric field due to the uniformly charged spherical shell is zero at all points inside the shell .

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

FULL MARKS-ELECTROSTATICS -Textual Evaluation Solved ( III. Long Answer Questions: )

Home
Ask Doubt
Profile