Obtain the expression for electric field due to an infinitely long charged wire . Solution in Tamil

Video Solution

Text Solution

Verified by Experts

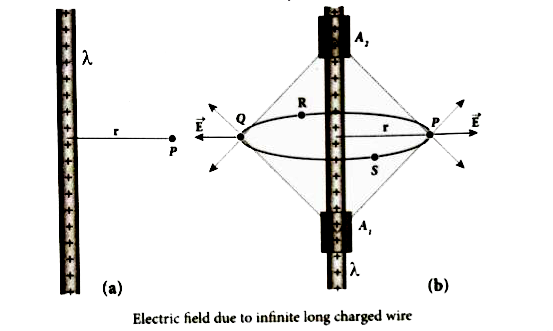
Electric field due to an infinitely long charged wire: Consider an infinitely long straight wire having uniform linear charge density $λ$ . Let P be a point located at a perpendicular distance r from the wire. The electric at the point P can be found using Gauss law . We choose two small charge element $A_{1}$ and $A_{2}$ on the wire which are at equal distance from the point P. The resultant electric field due to these two charge elements points radially away from the charged wire and the magnitude of electric field is same at all points on the circle of radius r. From this property. We can infer that the charged wire possesses a cylindrical symmetry.

Let us choose a cylindrical Gaussian surface of radius r and length L . The total electric flux in this closed surface is
$Φ_{E} = \oint \to E . d \to A$
$Φ_{E} = \oint \oint Curved surface \to E . d \to A + \int Top surface \to E . d \to A + \int Bottom surfac \to E . d \to A$
It is seen that for the curved surface $\to E$ is perpendicular to $\to A$ and $\to E . d \to A$ = 0
Substituting these value in the equation (2) and applying Gauss law to the cylindrical surfaces we hav
$Φ_{E} = \int Curved surface E d A = \frac{Q_{encl}}{ε_{0}}$
Since the magnitude of the electric field for the entire curved surface is constant E is taken out of the integration and $Q_{encl}$ given by
$Q_{encl} = λ L .$
$E \int Curved surface d A = \frac{λ L}{ε_{0}}$

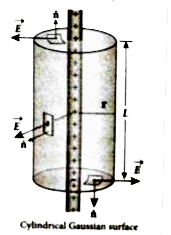
Here $Φ_{E} = \int Curved surface d A$ = total area of the curved surface = $2 π L$ . Substituting this in equation (4) We get
$E .2 π r L = \frac{λ L}{ε_{0}} (or) E = \frac{1}{2 π ε_{0}} \frac{λ}{r}$
In vector form $\to E = \frac{1}{2 π ε_{0}} \frac{λ}{r} ˆ r$
The electric field due to the infinite charged wire depends on $\frac{1}{r}$ rather than $\frac{1}{r^{2}}$ for a point charge . Equation (6) indicates that the electric field ios always along the perpendicular direction ( r) to wire . In fact if $λ >$ 0 then $\to E$ points perpendicular outward $(ˆ r)$ from the wire and if $λ < 0$ then $\to E$ points perpendicular inward $(- ˆ r)$ .

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

FULL MARKS-ELECTROSTATICS -Textual Evaluation Solved ( III. Long Answer Questions: )

Home
Ask Doubt
Profile