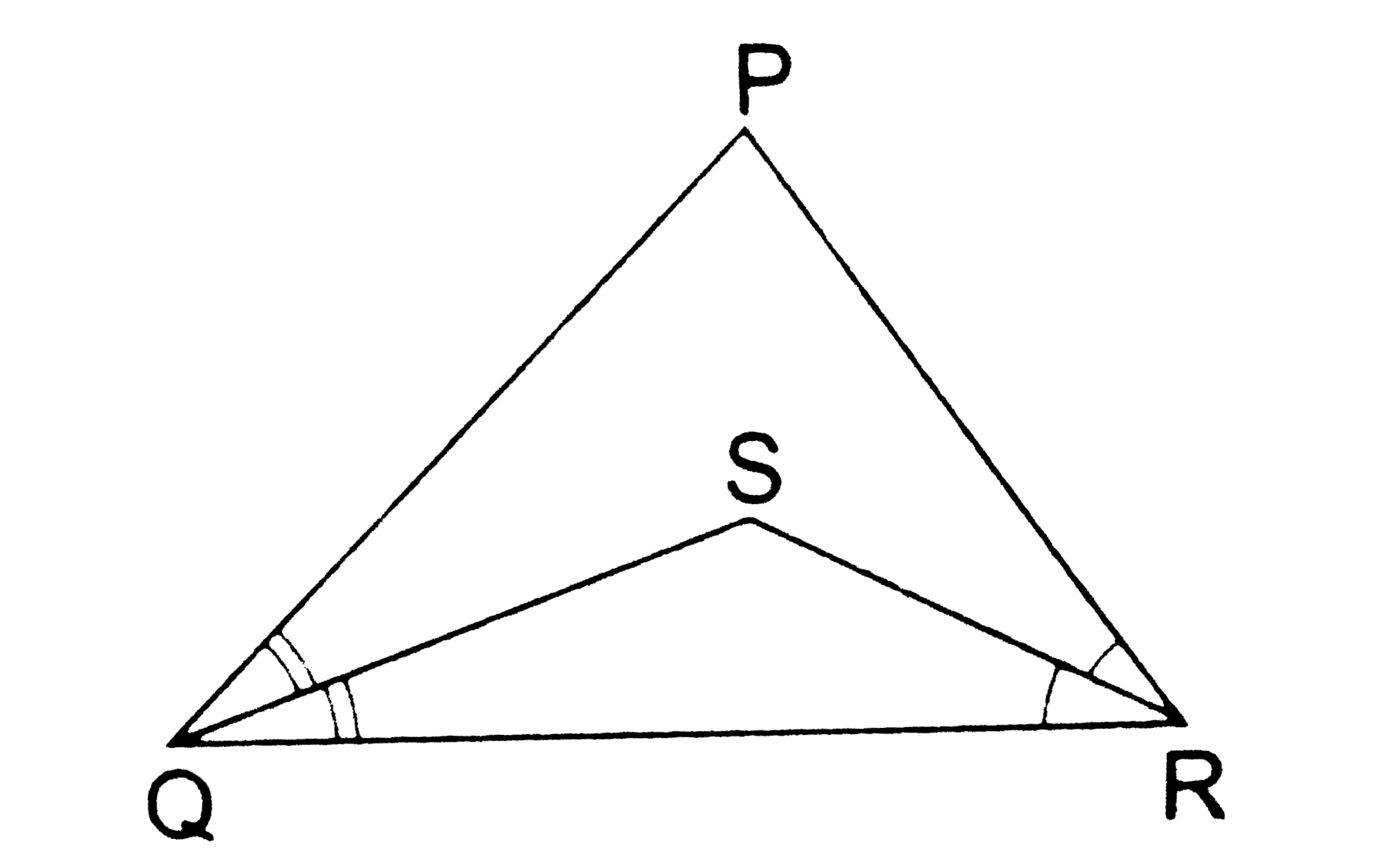
In the figure below, 2∠P=∠QOR. OQ and OR are bisectors of ∠Qand∠R respectively. Find ∠P.

A
60∘
B
70∘
C
40∘
D
80∘
Video Solution
Text Solution
The correct Answer is:A
2∠P=∠QOR
In ΔPQR,∠P+∠Q+∠R=180∘ .(1)
⇒∠Q+∠R=180∘−∠P
In ΔOQR,∠OQR+∠QOR+∠ORQ=180∘.
⇒∠Q2+2∠P+∠R2=180∘ (2).
⇒2∠P+180∘−∠P2=180∘
∠P=60∘
Hence, the correct option is (a).
|
Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Test-1
Explore 12 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Test-2
Explore 12 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level-2
Explore 26 Videos
- FORMULASBook:PEARSON IIT JEE FOUNDATIONChapter:FORMULASExercise:ASSESSMENT TESTS (Test 2)
Explore 8 Videos
- INDICES Book:PEARSON IIT JEE FOUNDATIONChapter:INDICES Exercise:Test -2
Explore 12 Videos
Similar Questions
Knowledge Check
In the figure below 2∠P=∠QOP, OQ and OR are bisectors of ∠Qand∠R respectively. Find ∠P
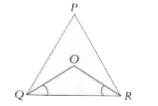 A60∘B70∘C40∘D80∘
A60∘B70∘C40∘D80∘In the following figure ∠BOP=2x∘,∠AOP=2y∘OCandOD are angle bisectors of ∠BOP and ∠AOP respectively.
Find the value of ∠COD:
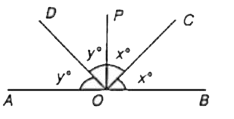 A75∘B90∘C106∘D220∘
A75∘B90∘C106∘D220∘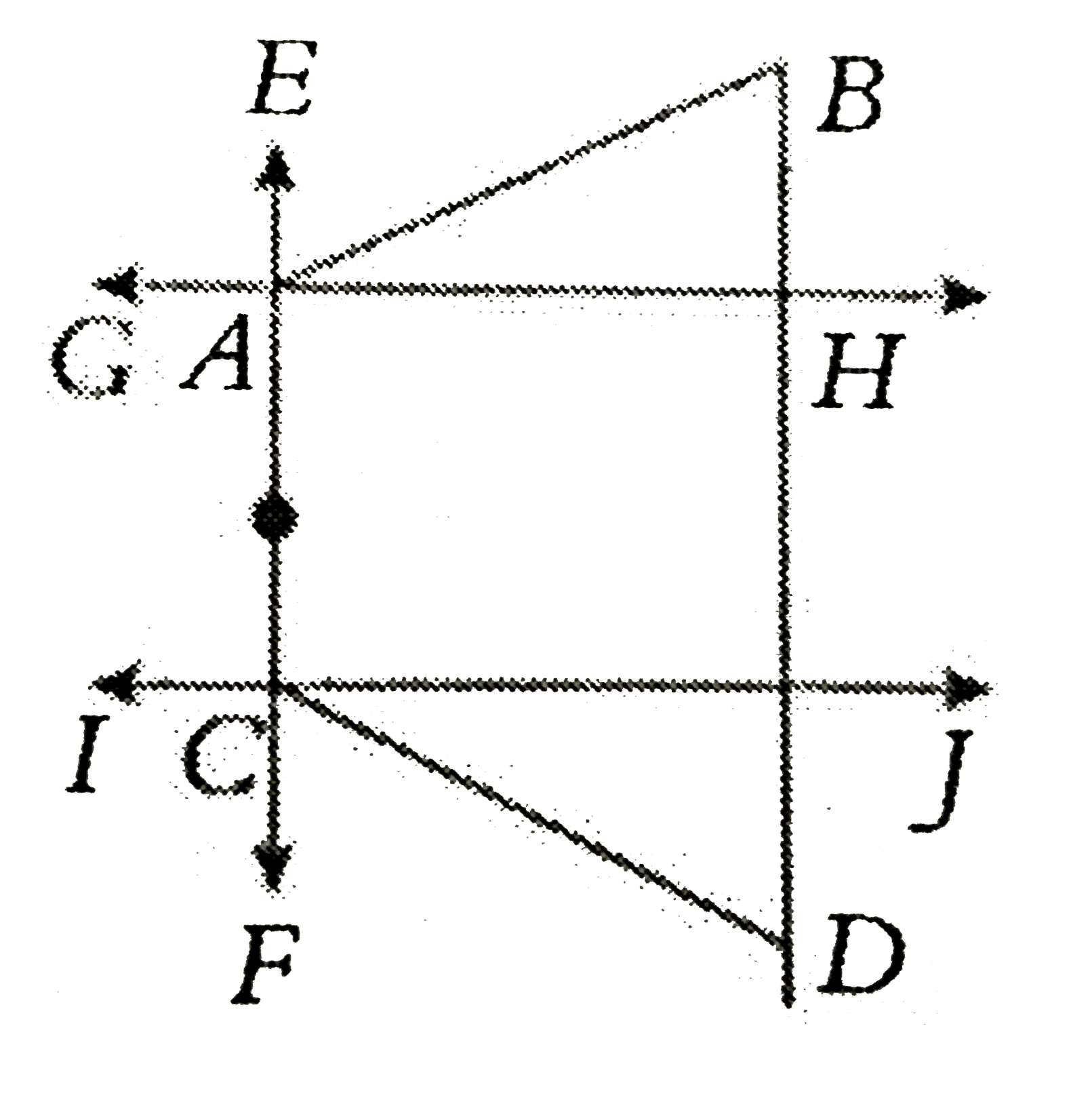
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.A80∘B90∘C100∘D110∘
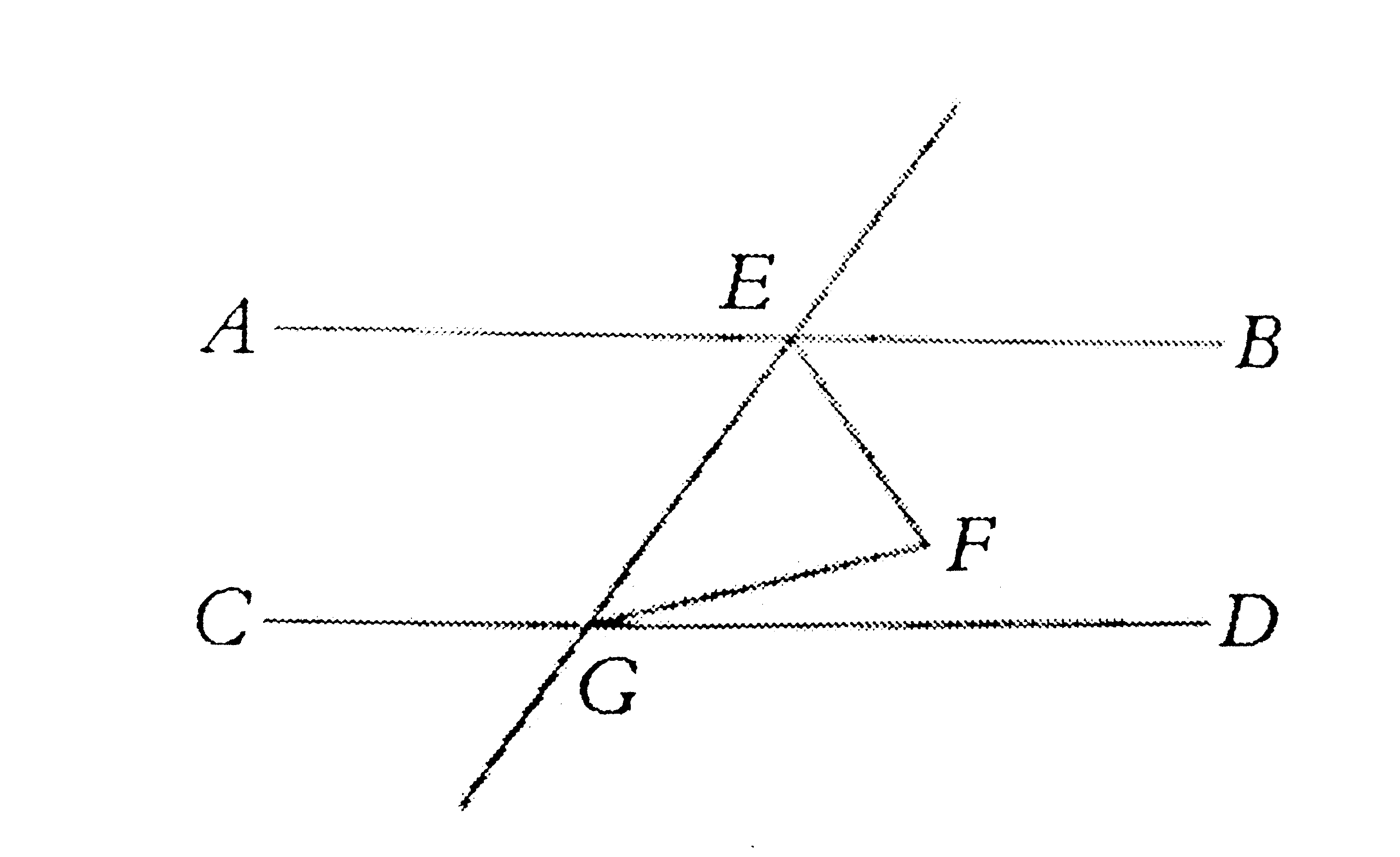
In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.
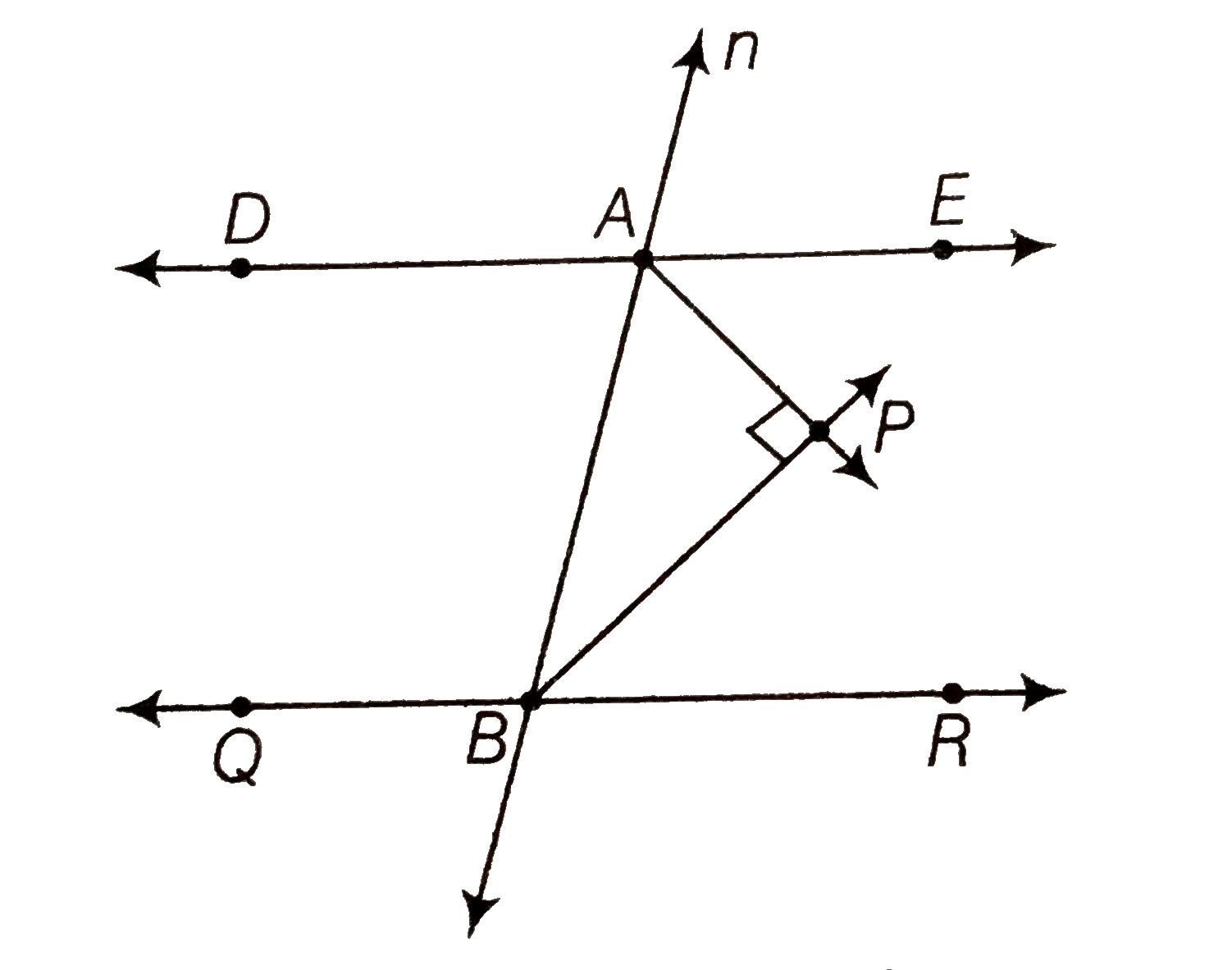
View SolutionIn the figure, DE|| QR and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
View Solution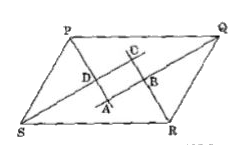
In the figure given above, PQRS is parallelogram. If AP, AQ, OR, CS are bisectors of ∠P,∠Q,∠R and ∠S respectively, then ABCD is a
View Solution
In the figure above, ∠Q=2∠Sand∠QRS=2∠RPS. Find ∠RPS+∠S
View SolutionIn the given figure, OD and OE are bisectors of ΔCDE and ΔDEB respectively. Find the measures of <1, <2,<3,<4
View Solution