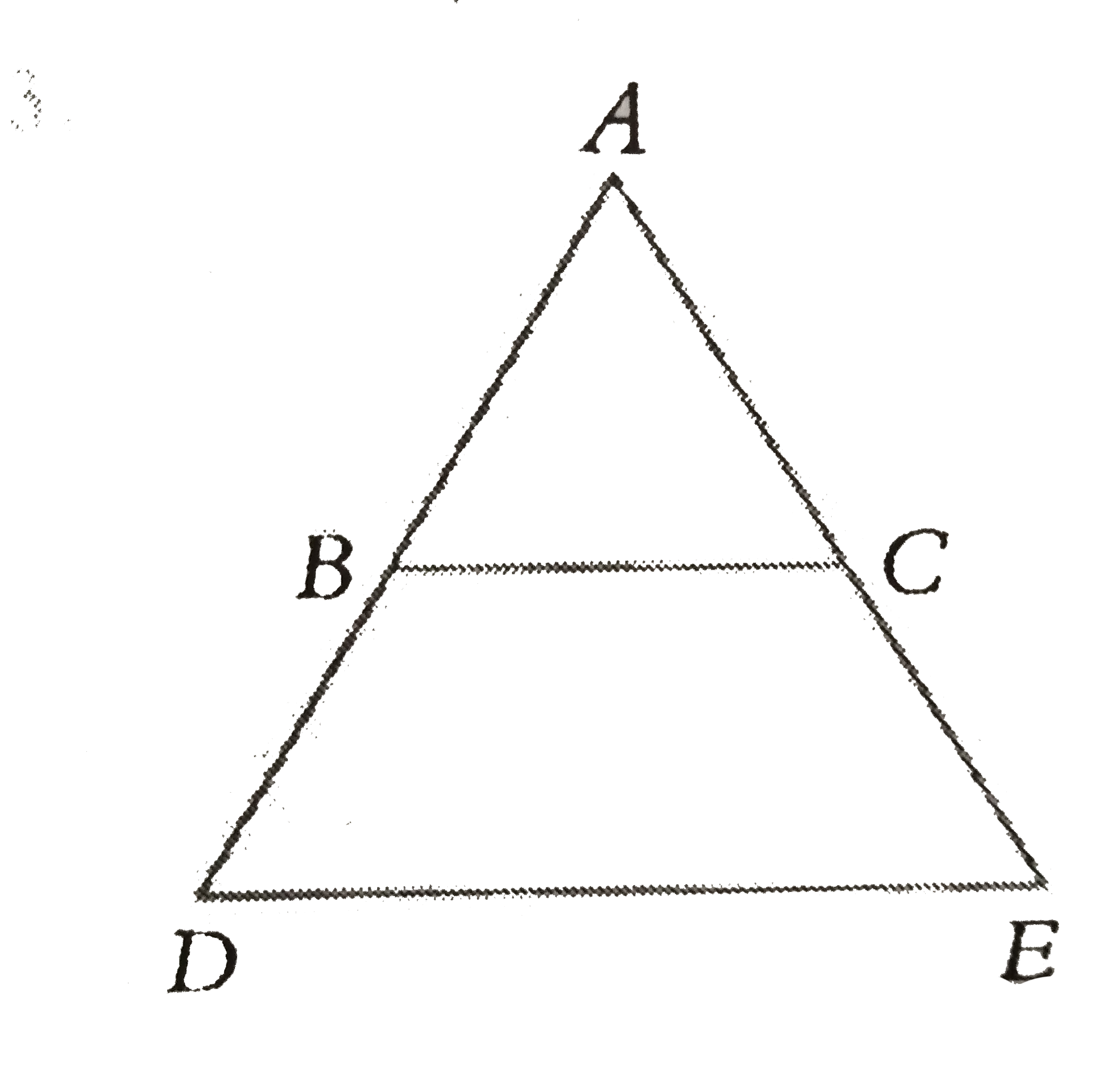
In the figure above, BC || DE and ∠ABC=∠CED.∠A=∠ACB−30∘. Find ∠A.
A
40∘
B
50∘
C
45∘
D
55∘
Video Solution
Text Solution
The correct Answer is:A
Given, BC∣∣DE,∠ABC=∠CED,and∠A=∠ACB−30∘
⇒∠ACB=∠CED
⇒∠ABC=∠ACB(∵BC∣∣DE)
In ΔABC,
∠A+∠ABC+∠ACB=180∘
∠ACB−30∘+∠ACB+∠ACB=180∘
⇒2∠ACB=210∘⇒∠ACB=70
∴∠A=40∘
Hence, the correct option is (a).
|
Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Test-1
Explore 12 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Test-2
Explore 12 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level-2
Explore 26 Videos
- FORMULASBook:PEARSON IIT JEE FOUNDATIONChapter:FORMULASExercise:ASSESSMENT TESTS (Test 2)
Explore 8 Videos
- INDICES Book:PEARSON IIT JEE FOUNDATIONChapter:INDICES Exercise:Test -2
Explore 12 Videos
Similar Questions
Knowledge Check
In an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
A36∘B32∘C28∘D40∘In ΔABC,2∠A=3∠B=6∠C, then find ∠A.
A90∘B30∘C60∘D45∘In the figure , l||m such that ∠A=110∘ & ∠B=130∘ then ∠ACB is
A50∘B60∘C70∘D120∘
In a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionIn a △ABC if ∠A=72∘ and ∠B=63∘,find ∠C
View Solution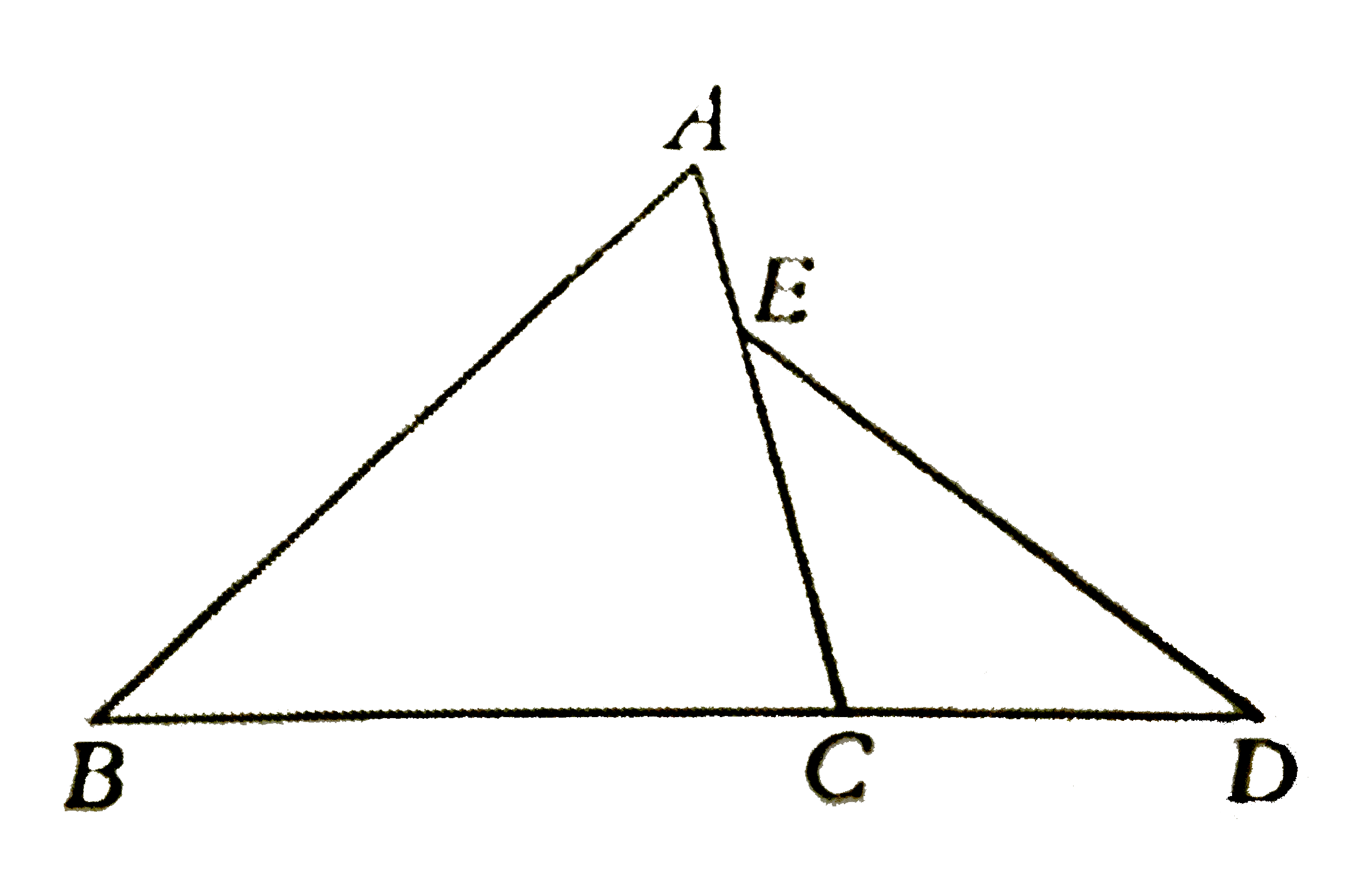
In the figure above, BC=AC, CD=CE. If ∠ABC=50∘, then find ∠CED.
View SolutionIn the figure, if ∠A=100∘ then ∠C=?
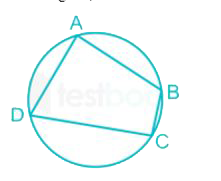
View Solution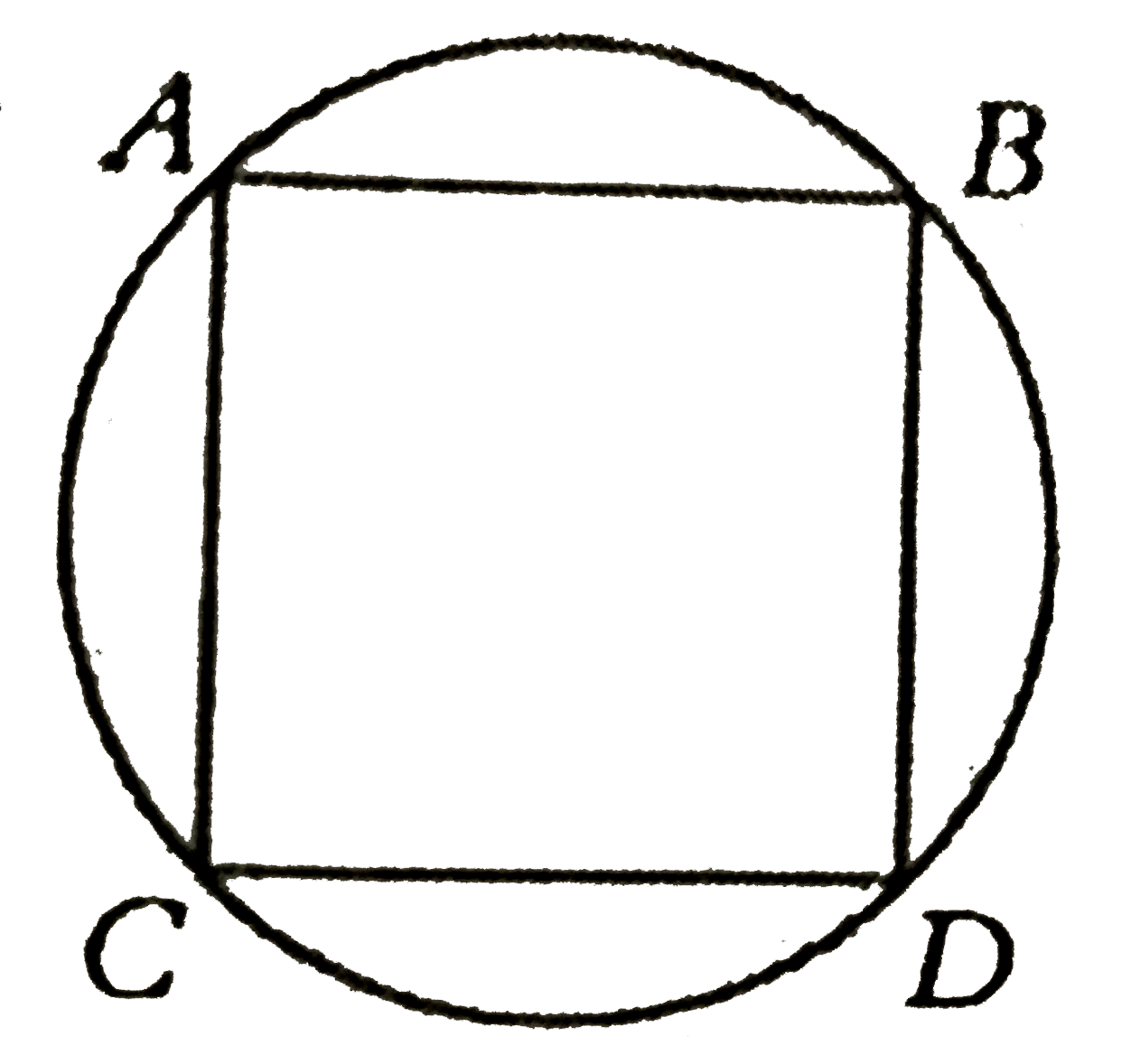
In the figure above (not to scale), AB=CD and ∠A=100∘. ∠C=
View Solution