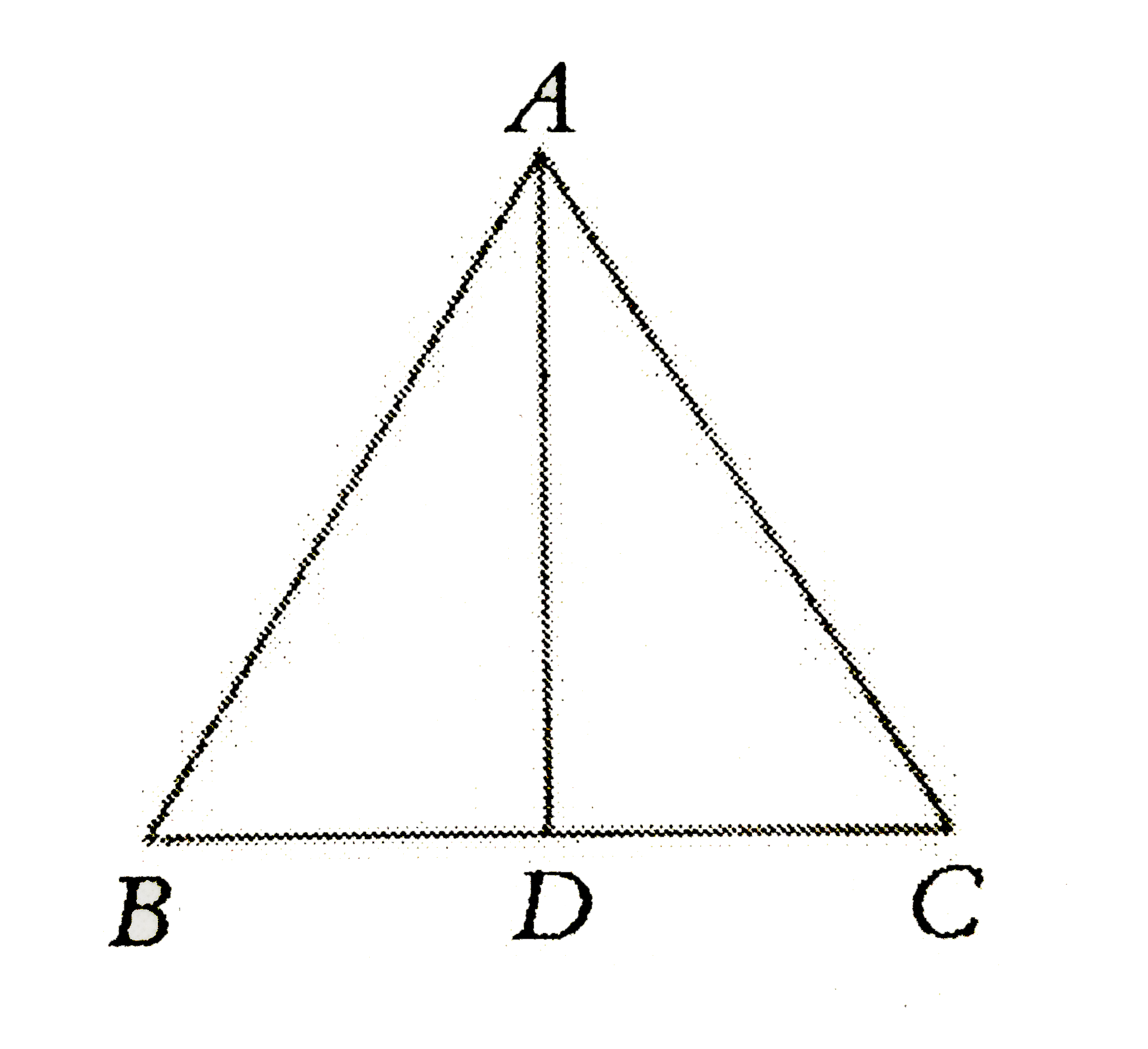
In the figure above, BD is the altitude drawn to AC. Triangles ABD and CBD are congruent if _________
AB=BC
AD=CD
Either (a) or (b)
None of these
The correct Answer is:C
¯¯¯¯¯¯BD⊥¯¯¯¯¯¯ACAC⇒∠BDC=∠BDA=90∘
BD is the common side of ΔABDandΔCBD.
(i) If AB=BC ,
ΔABD≅ΔCBD ( by RHS ).
(ii) If AD=CD,
ΔABD≅ΔCBD (by SAS).
Hence, the correct option is ( c).
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-112videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-212videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-226videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)8videos
FORMULAS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -212videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
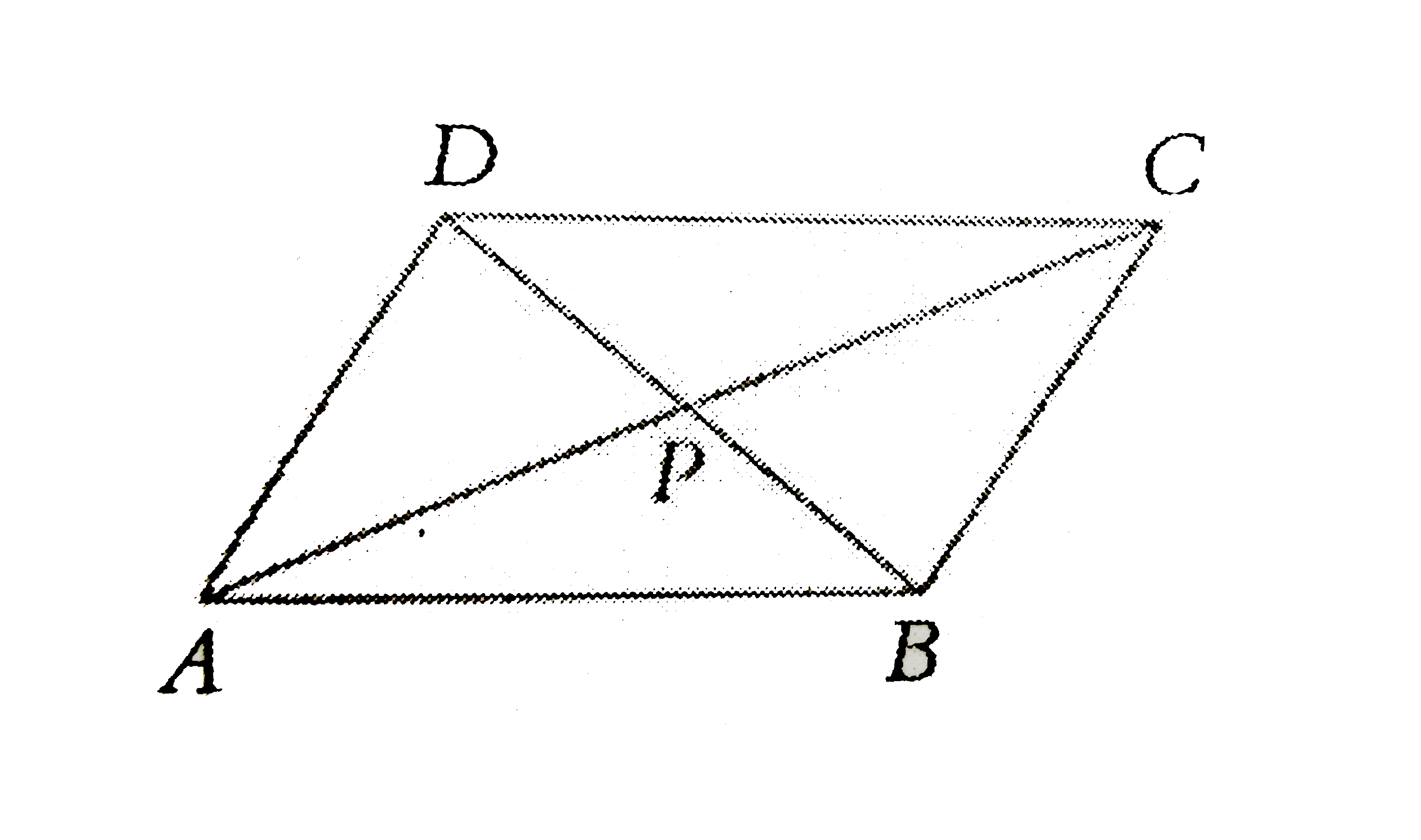
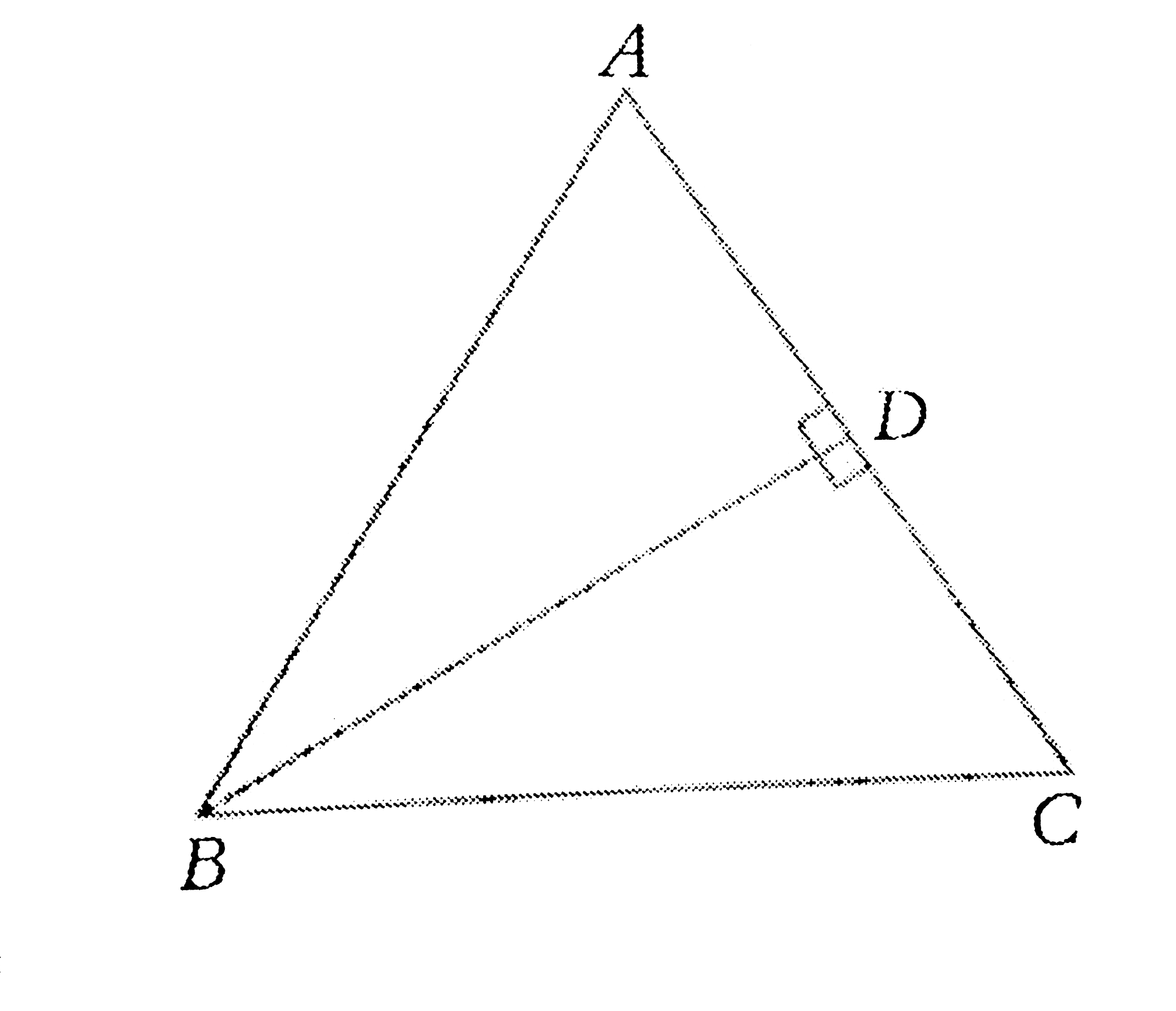
In the figure above, ABCD is a parallelogram , and if AC=30 cm and BD=20 cm, find CP+DP.A5B7C24D12 - Question 2 - Select One
In the given figure, BD and CE are the altitudes of triangle ABC such that BD = CE, then
ΔCBD is congruent toAΔCBEBΔBCECΔBECDΔECB - Question 3 - Select One
In the given figure, BD and CE are the altitudes of triangle ABC such that BD = CE, then
∠DCB=A∠EBCB∠ECBC∠ABDD∠DBC
Draw a labelled figure showing information given in the following statement : If the altitudes drawn on two sides of a triangle are congruent then those two sides are congruent . Also write the antecedent and the consequent part with respect to the figure drawn.
View Solution-
In the figure above, ABCD is a parallelogram , and if AC=30 cm and BD=20 cm, find CP+DP.View Solution In the given figure, prove that AC=BD.
View Solution-
In the figure above, ABCD is a parallelogram , and if AC=30 cm and BD=20 cm, find CP+DP.View Solution In the figure given below, ABC is a triangle with AB = BC and D is an interior point of the triangle ABC such that ∠DAC=∠DCA.
Consider the following statements :
1. Triangle ADC is an isosceles triangle.
2. Dis the centroid of the triangle ABC.
3. Triangle ABD is congruent to the triangle CBD.
Which of the above statements are correct ?View Solution