The area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
α=e2+1
α=e2−2
β=1+e−1
β=1+e−2
The correct Answer is:A, D
Solving given curves y=1x2,y=14(x−1), we get
x2=4(x−1)⇒(x−2)2=0
So, curves touch other at x=2.
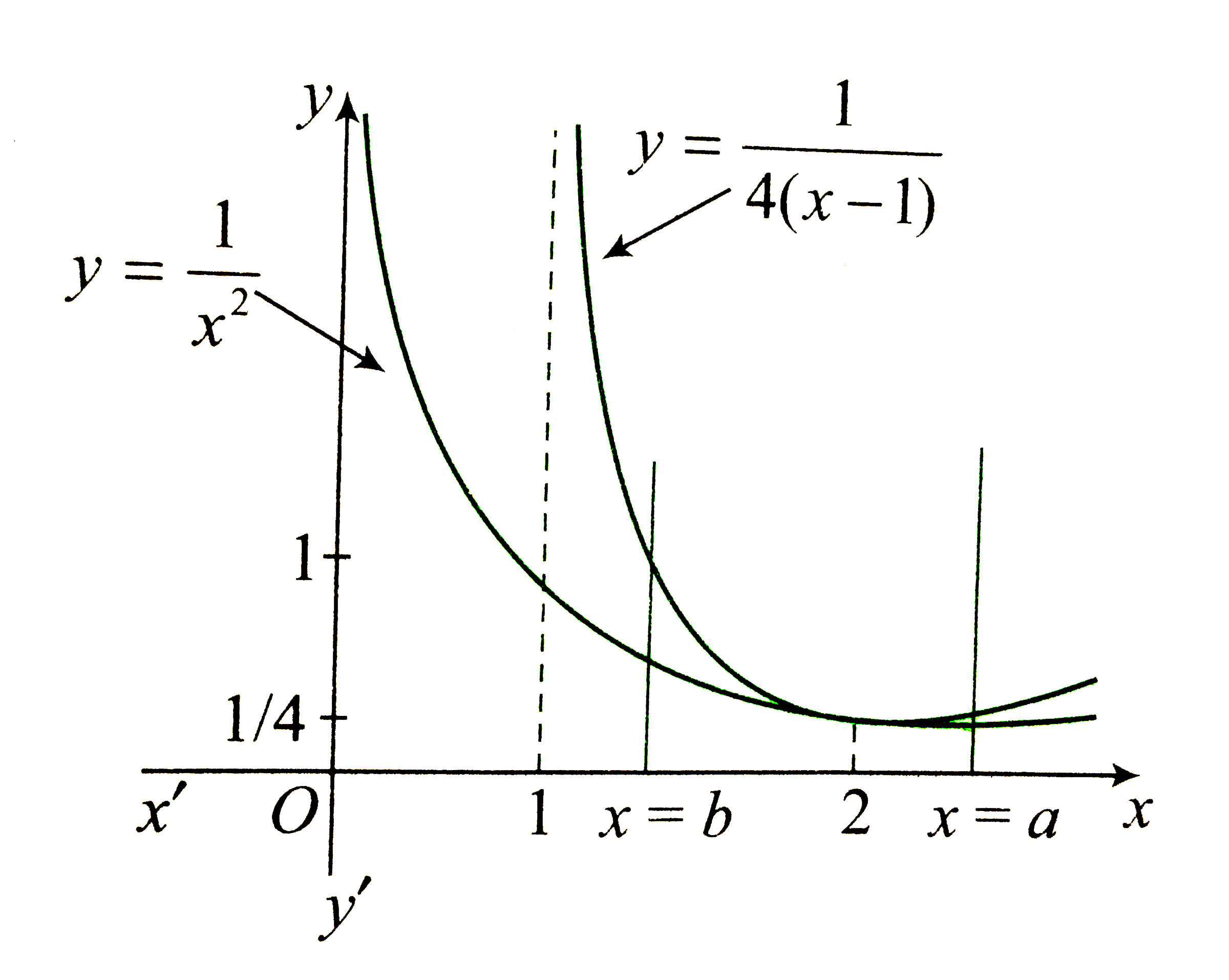
∴ A=a∫2(14(x−1)−1x2)dx=1a
⇒[14log(x−1)+1x]a2=1a
⇒ 14log(a−1)+1a−12=1a
⇒ log(a−1)=2
⇒ a=e2+1
Also 1−1b=2∫0(14(x−1)−1x2)dx
⇒ b=1+e−2
Topper's Solved these Questions
- AREABook:CENGAGEChapter:AREAExercise:Exercise (Comprehension)
Explore 21 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise (Matrix)
Explore 4 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise (Single)
Explore 40 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGEChapter:APPLICATIONS OF DERIVATIVESExercise:Question Bank
Explore 29 Videos
- AREA UNDER CURVESBook:CENGAGEChapter:AREA UNDER CURVESExercise:Question Bank
Explore 20 Videos
Similar Questions
Knowledge Check
The area of the region bounded by the curves y2=8x and y = x (in sq unit) is
A643B323C163D83
The area bounded by the curves y=x3−x and y=x2+x is (In sq, units)
View Solution" The area bounded by the curve "y=x(x-3)^(2)" and "y=x" is (in sq.units "
View SolutionThe area bounded by the curve y=4x−x2 and x-axis is (A) 307 sq. units (B) 317 sq. units (C) 323 sq. units (D) 343 sq. units
View SolutionThe area bounded by curves y2=4x and y=2x is ......... sq units
View SolutionThe area bounded by the curves y=logex and y=(logex)2 is (A) e−2 sq. units (B) 3−e sq. units (C) e sq. units (D) e−1 sq. units
View SolutionArea of the region bounded by the curve y2=4x, y-axis and the line y=3 is (A) 2 sq. units (B) 94 sq. units (C) 6√3 sq. units (D) none of these
View SolutionThe area bounded by the curve y=logex, the x-axis and the line x=e is (A) e sq. units (B) 1 sq. unit (C) (1−1e) sq. units (D) (1+1e) sq. units
View Solution

