Question

Which of the following have the same bounded area
$f\left(x\right)=s\in x,g\left(x\right)={\sin }^{2}x,where0\le x\le 10\pi$

$f\left(x\right)=s\in x,g\left(x\right)=|s\in x|,where0\le x\le 20\pi$

$f\left(x\right)=|s\in x|,g\left(x\right)={\sin }^{3}x,where0\le x\le 10\pi$

$f\left(x\right)=s\in x,g\left(x\right)={\sin }^{4}x,where0\le x\le 10\pi$

Options

A. `f(x)= sin x, g(x) = sin^(2)x," where "0lexle 10 pi`
B. `f(x)= sin x, g(x) = |sin |," where "0le x le 20 pi`
C. `f(x)=|sin|,g(x)=sin^(3)x," where "0lexle10 pi`
D. `f(x)=sin x, g(x)=sin^(4)x," where "0le xle 10 pi`

Answer

A::C::D

Explanation

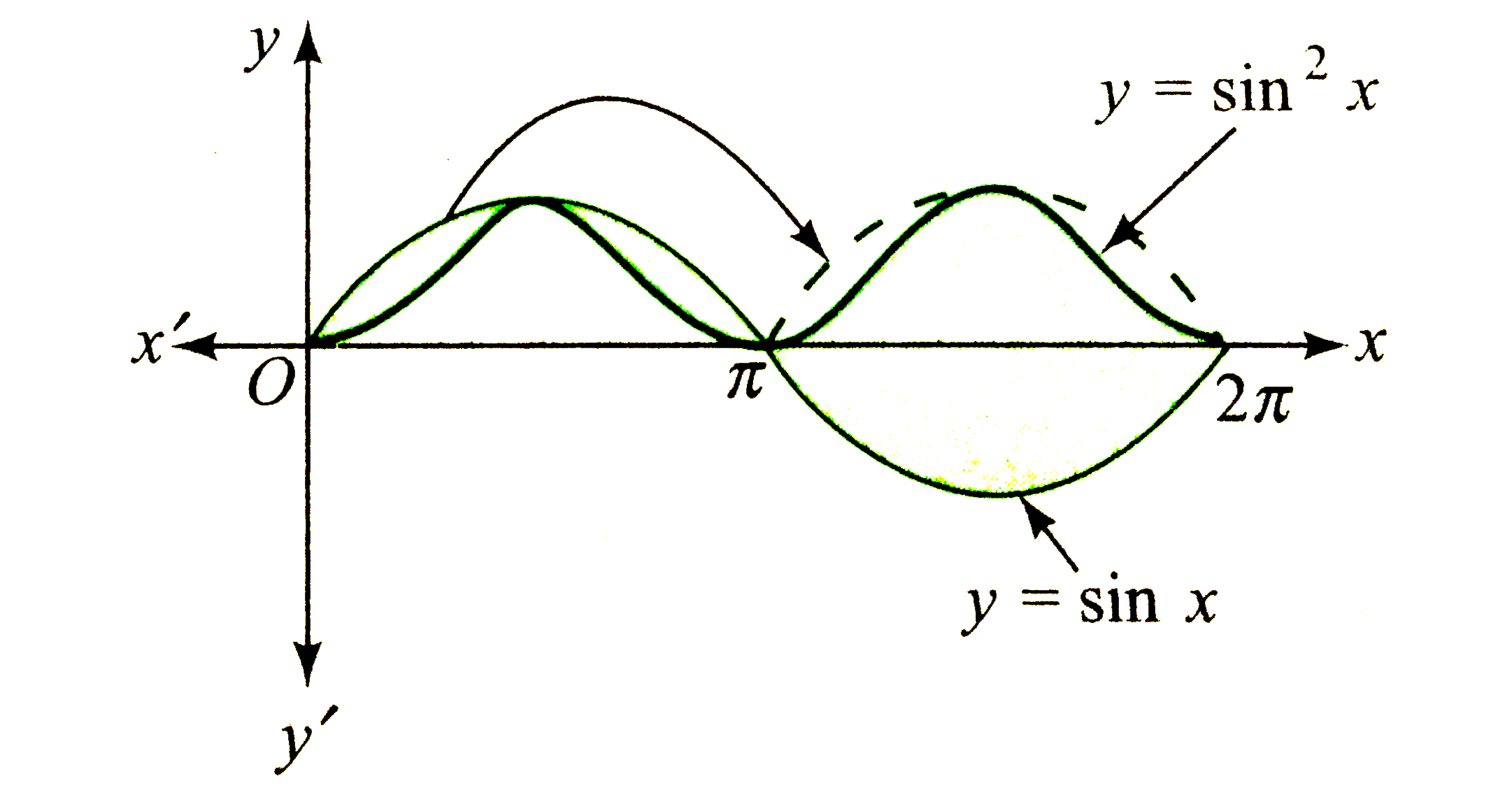
We know that area bounded by `y= sin x` and x-axis for ` x in [0,pi]` is 2 sq. units.
Then area bounded by `y= sin x and y=sin^(2)x` is 4 sq. units for `x in [0,2pi]`.
Then for `x in [0,10pi]`, the area bounded is 20 sq. units.

The area bounded by y= sin x and y = `|sin x |" for " x in [0, 2pi]` is 4 sq. units.
Then for `x in [0,20pi],` the area bounded is 40 sq. units.

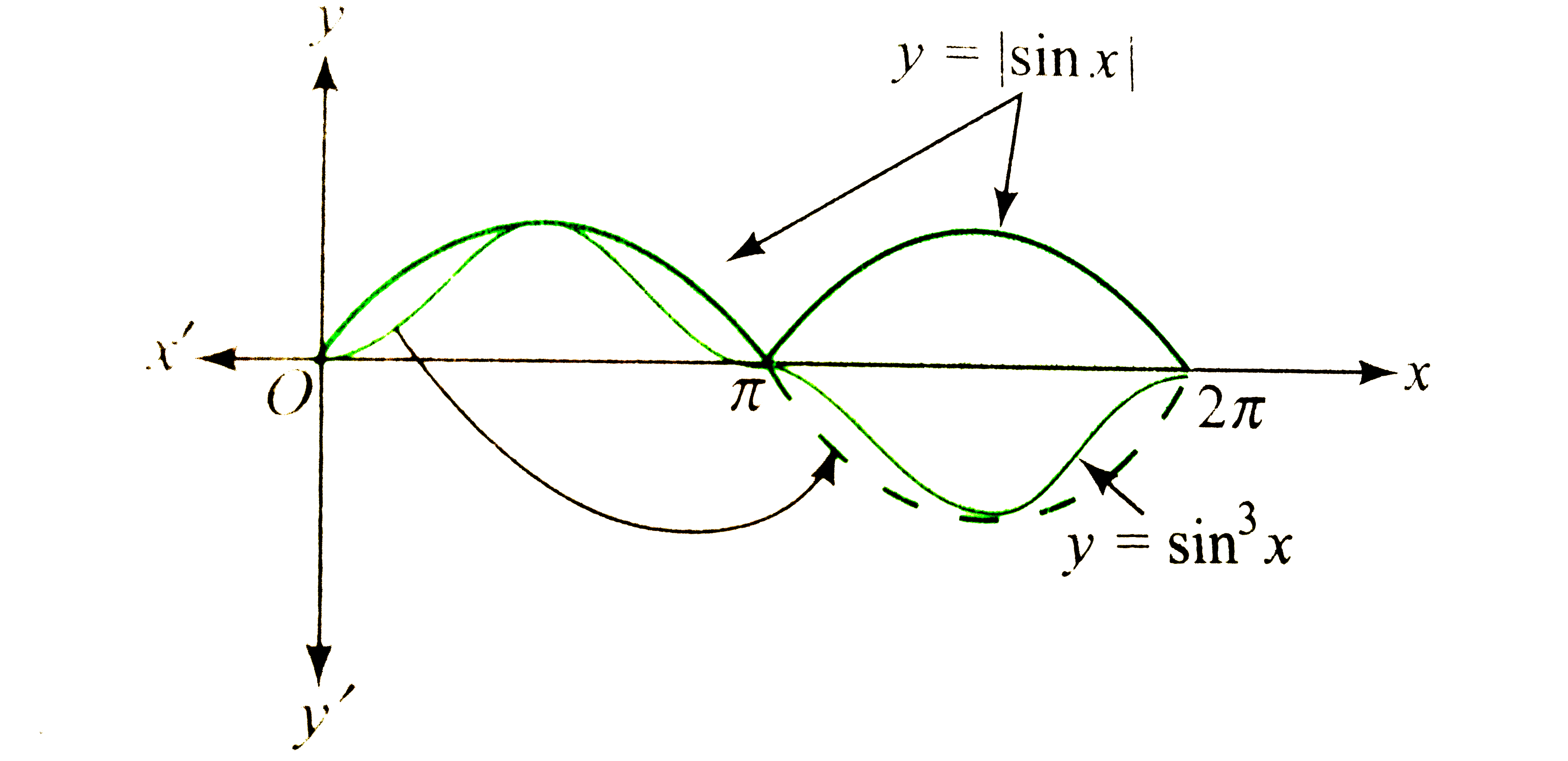
The area bounded by `y= sin x and y=sin^(3)x" for "x in [0,2pi]` is 4 sq units.
Then for `x in [0,10 pi],` the area bounded is 20 sq. units. Similarly, the area bounded by `y= sin x and y=sin^(4)x" for "x in [0,10pi]` is 20 sq. units.