A charged capacitor is carefully pulled apart into its component pieces. Do we need to supply the charge to the capacitor again when it is reassembled?
To determine whether we need to supply charge to a capacitor again when it is reassembled after being pulled apart into its component pieces, we need to consider the nature of the materials used during the separation process.
1. Understanding the Capacitor: A capacitor consists of two conductive plates separated by an insulating material. When charged, one plate holds a positive charge (+Q), while the other holds an equal negative charge (-Q).
2. Separation of Plates: When we carefully pull apart the capacitor into its component pieces, we need to consider how we are separating the plates. The method of separation is crucial to understanding the charge distribution after reassembly.
3. Using Non-Conducting Material: If we use a non-conducting material (insulator) to separate the plates, the charges on the plates will remain fixed. The positive charge (+Q) will stay on one plate, and the negative charge (-Q) will stay on the other plate.
4. Reassembling the Capacitor: When we reassemble the capacitor after using a non-conducting material, the charge distribution remains unchanged. Therefore, the capacitor retains its original charge, and there is no need to supply additional charge.
5. Using Conducting Material: If we were to use a conducting material to separate the plates, the situation would be different. Charges would redistribute themselves due to the conductive nature of the material. In this case, when reassembling the capacitor, the charge may not be the same as before, and we might need to supply charge again to achieve the original state.
6. Conclusion: In summary, if a non-conducting material is used to separate the capacitor plates, we do not need to supply charge again upon reassembly. However, if a conducting material is used, the charge distribution may change, and we may need to supply charge again.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Tough & Tricky PROBLEMS
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Textbook Exercise)
Explore 11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 5
Explore 18 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
Knowledge Check
Figure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?
 A6μCB8μCC10μCD12μC
A6μCB8μCC10μCD12μCDisplacement current exists between the plates of capacitor , when charge of the capacitor
Aremains constantBincreaseCdecreasesDzeroDisplacement current exists between the plates of capacitor , when charge of the capacitor
AConstantBMaximumCChangingDBoth (1) &(3)
Three capacitors are connected across a 45 V power supply as shown in fig.what is the charge on the 6μ F capacitor?
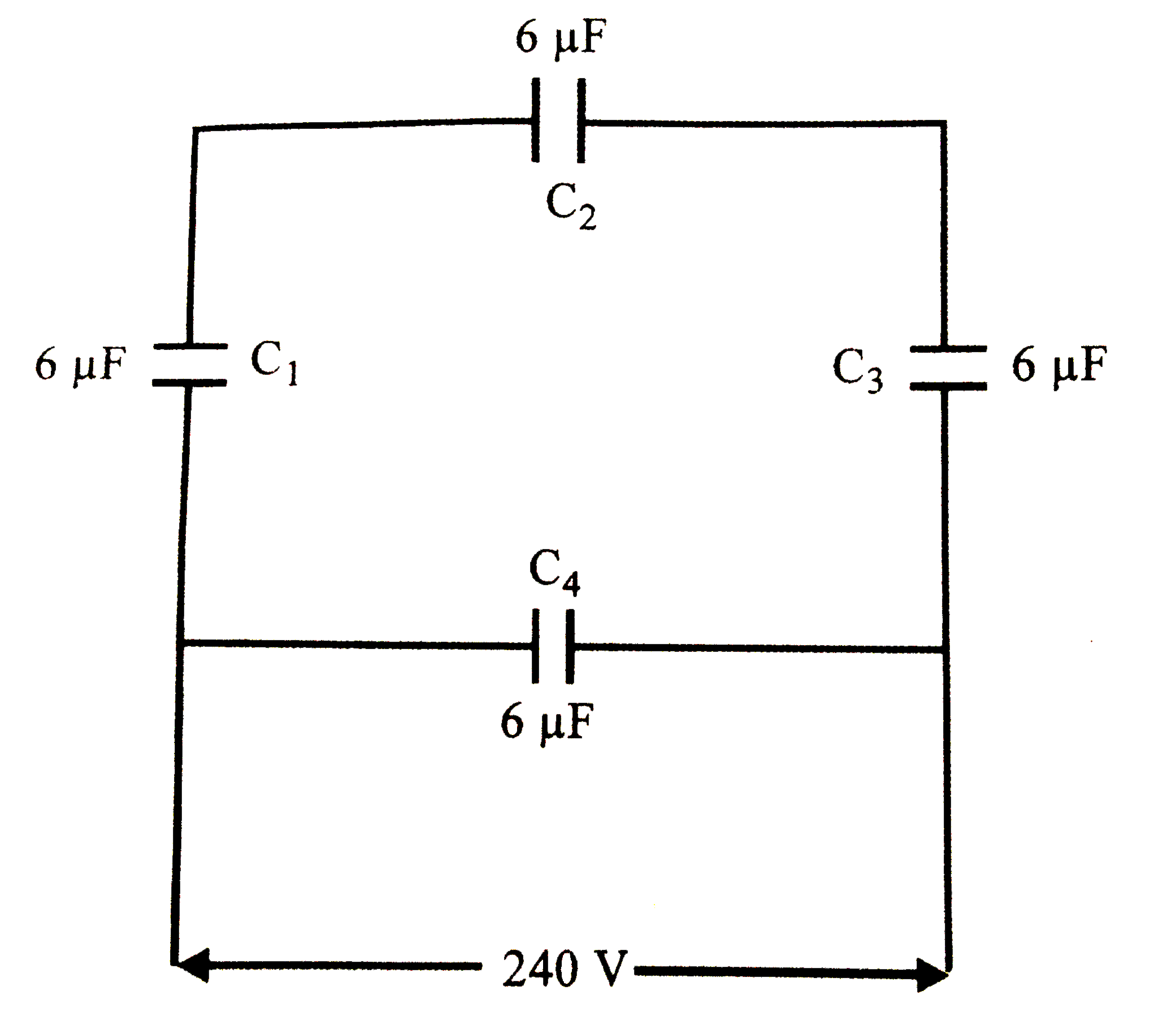
View SolutionA network of four capacitors of 6 μF each is connected to a 240 V supply. Determine the charge on each capacitor.
View SolutionA parallel plate capacitor is charged by connecting it to a battery. The battery is disconnected and the plates of the capacitor are pulled apart to make the separation between the plates twice. Again the capacitor is connected to the battery (with same polarity) then the potential difference between the plates increases when the plates are pulled apart (yes or not)
View SolutionWhen a charged capacitor is made to discharge through an inductance, the charge Q on the capacitor and the current i in the inducrtor vary sinusoidally. The phase different between Q and i is
View SolutionA charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
View Solution

