Two capacitors C1andC2 are connected to a voltage source in a parallel connection. Another arrangement of these capacitors is connected to the same voltage source but now in series. In which case the risk of handling the capacitors is more? Give reason in support of your answer.
To determine in which arrangement of capacitors (parallel or series) the risk of handling them is more, we need to analyze the energy stored in each configuration.
1. Understanding Capacitor Configurations:
- In a parallel connection, the total capacitance Ceq is given by:
Ceq=C1+C2
- In a series connection, the total capacitance Ceq is given by:
1Ceq=1C1+1C2⟹Ceq=C1C2C1+C2
2. Energy Stored in Capacitors:
- The energy U stored in a capacitor is given by the formula:
U=12CV2
- For the parallel connection, the energy U1 is:
U1=12(C1+C2)V2
- For the series connection, the energy U2 is:
U2=12(C1C2C1+C2)V2
3. Comparing Energies:
- To compare U1 and U2, we can find the ratio:
U1U2=12(C1+C2)V212(C1C2C1+C2)V2
- Simplifying this gives:
U1U2=(C1+C2)2C1C2
4. Using the Arithmetic and Geometric Mean Inequality:
- According to the inequality of arithmetic and geometric means:
C1+C22≥√C1C2
- Therefore, we can conclude:
C1+C2≥2√C1C2
- Squaring both sides gives:
(C1+C2)2≥4C1C2
- This implies:
(C1+C2)2C1C2≥4
5. Conclusion:
- Since U1U2>1, we find that U1>U2.
- This means that the energy stored in the parallel arrangement is greater than that in the series arrangement.
- Hence, the risk of handling the capacitors is more in the parallel connection because it stores more energy and is therefore more unstable.
- In a parallel connection, the total capacitance Ceq is given by:
Ceq=C1+C2
- In a series connection, the total capacitance Ceq is given by:
1Ceq=1C1+1C2⟹Ceq=C1C2C1+C2
- The energy U stored in a capacitor is given by the formula:
U=12CV2
- For the parallel connection, the energy U1 is:
U1=12(C1+C2)V2
- For the series connection, the energy U2 is:
U2=12(C1C2C1+C2)V2
- To compare U1 and U2, we can find the ratio:
U1U2=12(C1+C2)V212(C1C2C1+C2)V2
- Simplifying this gives:
U1U2=(C1+C2)2C1C2
- According to the inequality of arithmetic and geometric means:
C1+C22≥√C1C2
- Therefore, we can conclude:
C1+C2≥2√C1C2
- Squaring both sides gives:
(C1+C2)2≥4C1C2
- This implies:
(C1+C2)2C1C2≥4
- Since U1U2>1, we find that U1>U2.
- This means that the energy stored in the parallel arrangement is greater than that in the series arrangement.
- Hence, the risk of handling the capacitors is more in the parallel connection because it stores more energy and is therefore more unstable.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Tough & Tricky PROBLEMS
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 5
18 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
If there are n capacitors in parallel connected to V volt source, then the energy stored is equal to
A(a) CVB(b) 12nCV2C(c) CV2D(d) 12nCV2Which of the following is true for an ideal capacitor connected to a sinusoidal voltage source ?
ANeither the average power nor the average current is zeroBAverage current is zero but not the average powerCThe average power is zero, but not the average currentDBoth the average power and average current are zeroA diode is connected to 220V(rms) ac in series with a capacitor as shown in fig. The voltage across the capacitor is
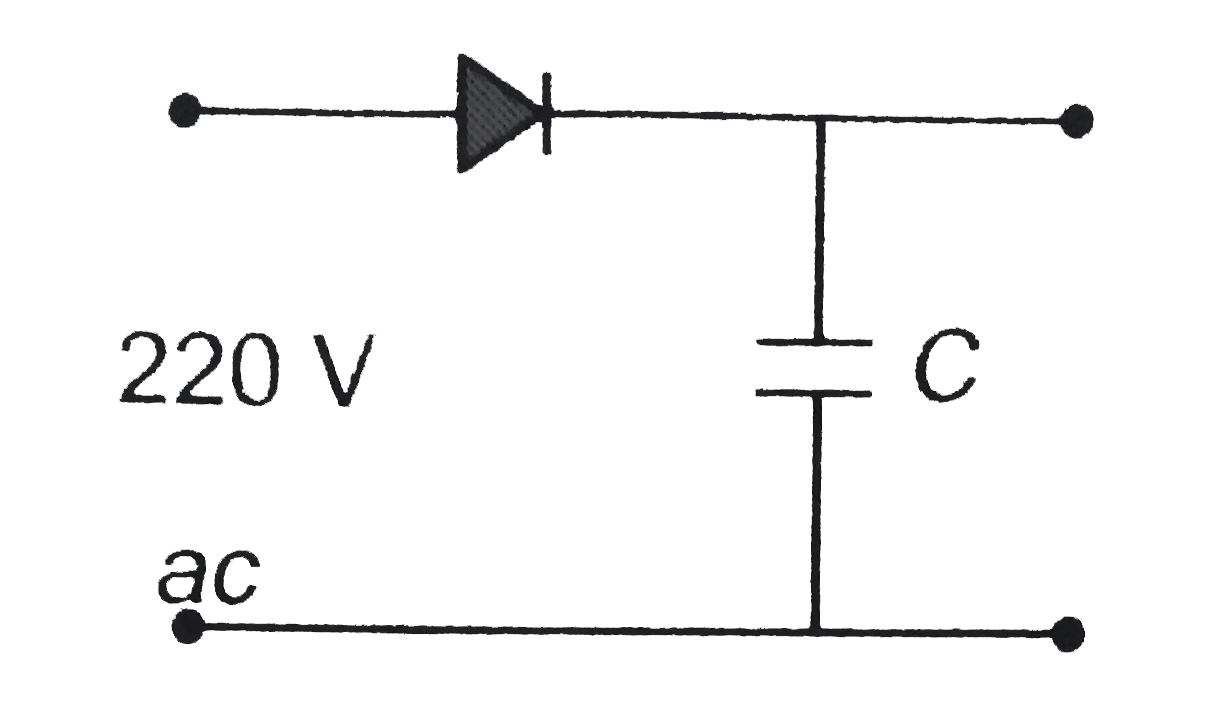 A220VB110VC311.1VD220√2V
A220VB110VC311.1VD220√2V
If n capacitors are connected in parallel to a V volt source then total energy of the system is:
View SolutionA parallel plate capacitor is first connected to a constant voltage source. It is then disconnected and ·then immersed in a liqnid dielectric, then:
View SolutionWhen a parallel plate capacitor is connected to a source of constant potential difference
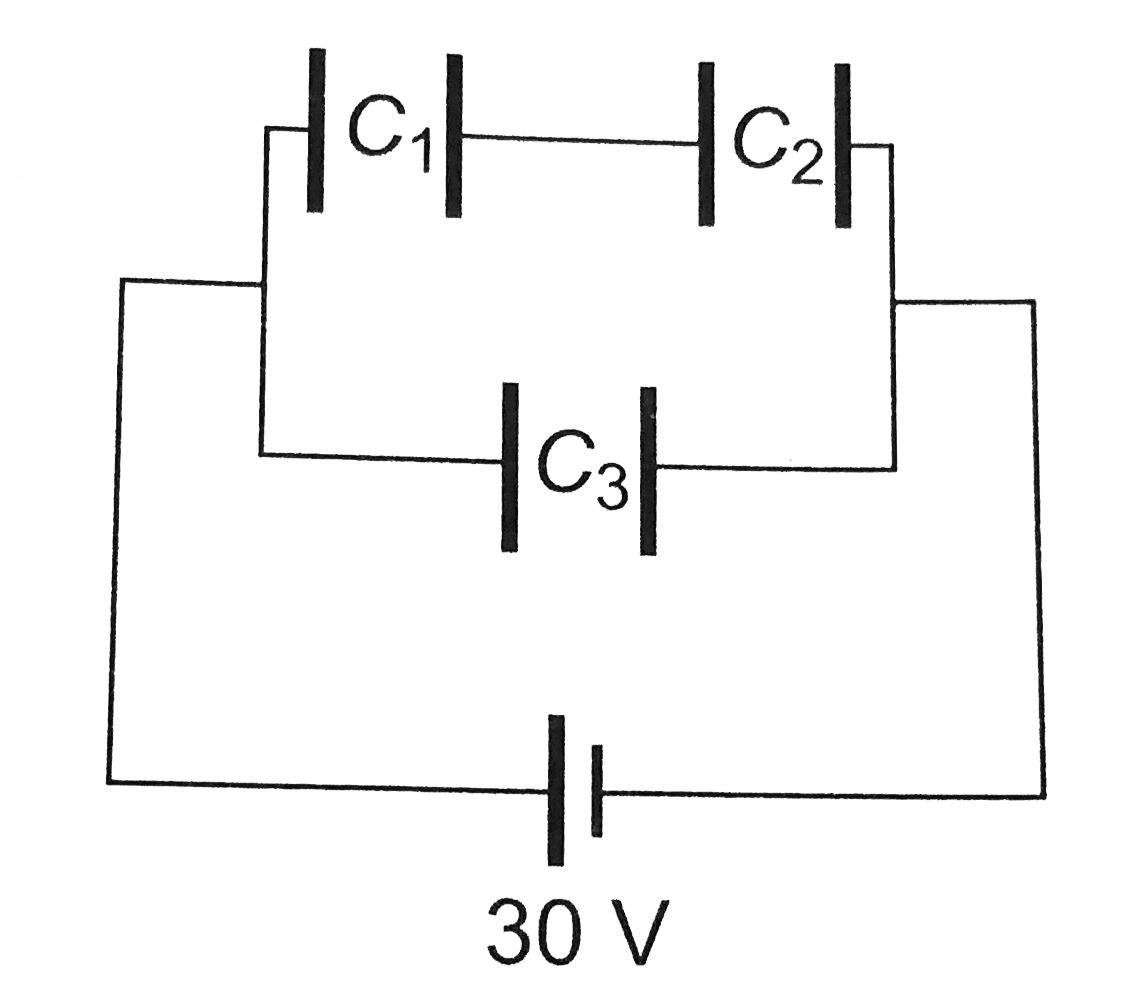
View SolutionTwo capacitors C1=3μF and C2=6μF in series, are connected in parallel to a third capacitor C3=4μF. This arrangement is then connected to a battery of e.m.f., =30V, as shown. The energy lost by the battery in charging the capacitors
View SolutionTwo capacitors having capacities C1andC2 are charged to voltages V1andV2 respectively. There will be no exchange of energy in connecting them in parallel, if
View Solution