There is an air capacitor with capacitance C, charged to a potential difference of V. If the capacitor is isolated from the battery after charging, and then a dielectric slab is inserted in between the plates of capacitor. How will the energy stored in this capacitor change?
To solve the problem step by step, let's analyze the situation involving the capacitor, the dielectric slab, and the energy stored in the capacitor.
Step 1: Understand the Initial Conditions
- The capacitor has a capacitance C and is charged to a potential difference V.
- The initial energy stored in the capacitor can be calculated using the formula:
Ui=12CV2
- Since the capacitor is isolated from the battery, the charge Q on the capacitor remains constant.
Step 2: Calculate the Initial Charge
- The charge Q on the capacitor can be expressed as:
Q=CV
Step 3: Insert the Dielectric Slab
- When a dielectric slab with dielectric constant K is inserted between the plates of the capacitor, the new capacitance C′ becomes:
C′=KC
- The dielectric increases the capacitance of the capacitor.
Step 4: Analyze the Charge and Voltage After Inserting the Dielectric
- Since the capacitor is isolated, the charge Q remains the same.
- The new voltage V′ across the capacitor after inserting the dielectric can be calculated using:
V′=QC′=QKC=CVKC=VK
Step 5: Calculate the Final Energy Stored in the Capacitor
- The new energy Uf stored in the capacitor after inserting the dielectric is given by:
Uf=12C′(V′)2
- Substituting C′ and V′:
Uf=12(KC)(VK)2=12(KC)(V2K2)=12CV2K
Step 6: Compare Initial and Final Energy
- The initial energy was:
Ui=12CV2
- The final energy is:
Uf=12CV2K
- Since K>1 (for a dielectric material), it follows that:
Uf<Ui
- Therefore, the energy stored in the capacitor decreases when the dielectric slab is inserted.
Final Result
- The energy stored in the capacitor decreases when a dielectric slab is inserted while the capacitor is isolated from the battery.
---
- The capacitor has a capacitance C and is charged to a potential difference V.
- The initial energy stored in the capacitor can be calculated using the formula:
Ui=12CV2
- Since the capacitor is isolated from the battery, the charge Q on the capacitor remains constant.
- The charge Q on the capacitor can be expressed as:
Q=CV
- When a dielectric slab with dielectric constant K is inserted between the plates of the capacitor, the new capacitance C′ becomes:
C′=KC
- The dielectric increases the capacitance of the capacitor.
- Since the capacitor is isolated, the charge Q remains the same.
- The new voltage V′ across the capacitor after inserting the dielectric can be calculated using:
V′=QC′=QKC=CVKC=VK
- The new energy Uf stored in the capacitor after inserting the dielectric is given by:
Uf=12C′(V′)2
- Substituting C′ and V′:
Uf=12(KC)(VK)2=12(KC)(V2K2)=12CV2K
- The initial energy was:
Ui=12CV2
- The final energy is:
Uf=12CV2K
- Since K>1 (for a dielectric material), it follows that:
Uf<Ui
- Therefore, the energy stored in the capacitor decreases when the dielectric slab is inserted.
- The energy stored in the capacitor decreases when a dielectric slab is inserted while the capacitor is isolated from the battery.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Tough & Tricky PROBLEMS
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Textbook Exercise)
Explore 11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 5
Explore 18 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
A capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the two capacitors before they are connected .
View Solution
Knowledge Check
A dielectric slab is inserted between the plates of an isolated charged capacitor. Which of the following quantities remain unchanged ?
AThe charge on the capacitorBThe stored energy in the capacitorCThe potential difference between the platesDThe electric field in the capacitorA dielectric slab is inserted between the plates of an isolated charged capacitor. Which of the following quantities remain unchanged ?
AThe charge on the capacitorBThe stored energy in the capacitorCThe potential difference between the platesDThe electric field in the capacitorA parallel plate capacitor is charged by a battery. The battery is removed and a thick glass slab is inserted between the plates. Now,
AThe capacity of the capacitor is increasedBThe electrical energy stored in the capacitor is decreasedCThe potential across the plate is decreasedDThe electric field between the plates is decreased.
If a capacitor connected to a battery is fully charged, then a dielectric (k) is inserted between plates then increase in the potential energy is
View SolutionThe answer to each of the following questions is a single-digit integer ranging from 0 to 9. Darken the correct digit.
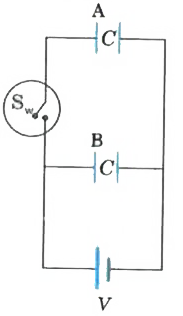
Two identical air capacitors of capacitance C are connected to a battery of EMF V and initially switch is closed for a long time. After the switch is opened, identical dielectric slabs are inserted in between the plates of both the capacitors and it is found that energy stored in capacitor B becomes nine times of the energy stored in capacitor A. What is the dielectric constant of the slab?
View SolutionA capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the parallel combination of two capacitors.
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionA capacitor of capacitance C is charged to potential difference V and then disconnected from the battery. The air dielectric of capacitor is replaced by another dielectric of dielectric constant K. The fractional decrease in energy of the capacitor is
View Solution

