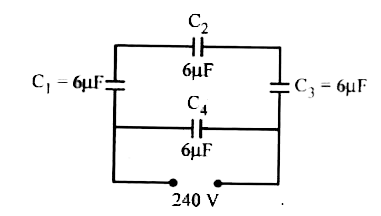
A network of four capacitors of 6 each is connected to a 240 V supply. Determine the charge on each capacitor.
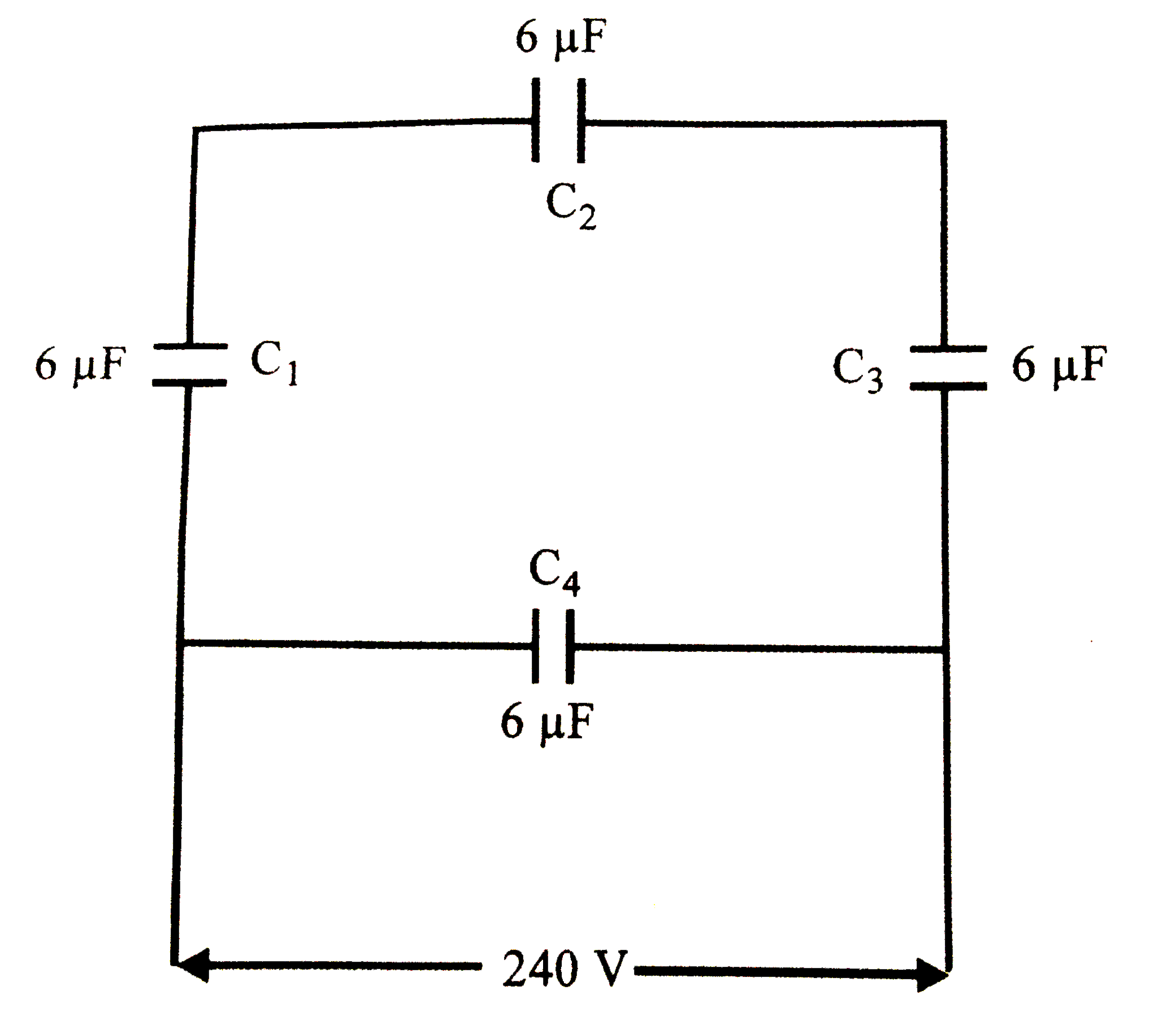
The capacitors and are connected in series. The equivalent capacitance C' is given by
Now, Total Capacitance,
In series the charge remains same. Therefore, the charge on and is given by
The charge on capacitance is given by
Topper's Solved these Questions
Similar Questions
A network of four 10μF capacitors is connected to a 500V supply as shown in Fig. Determine the (a) equivalent capacitance of the network and (b) charge on each capacitor.
View SolutionA network of four capacitors each of 12 μF capacitance is connected to a 500 V supply as shown in the Fig .

Determine charge on each capacitor .
View Solution
Knowledge Check
Figure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?
 A6μCB8μCC10μCD12μC
A6μCB8μCC10μCD12μC
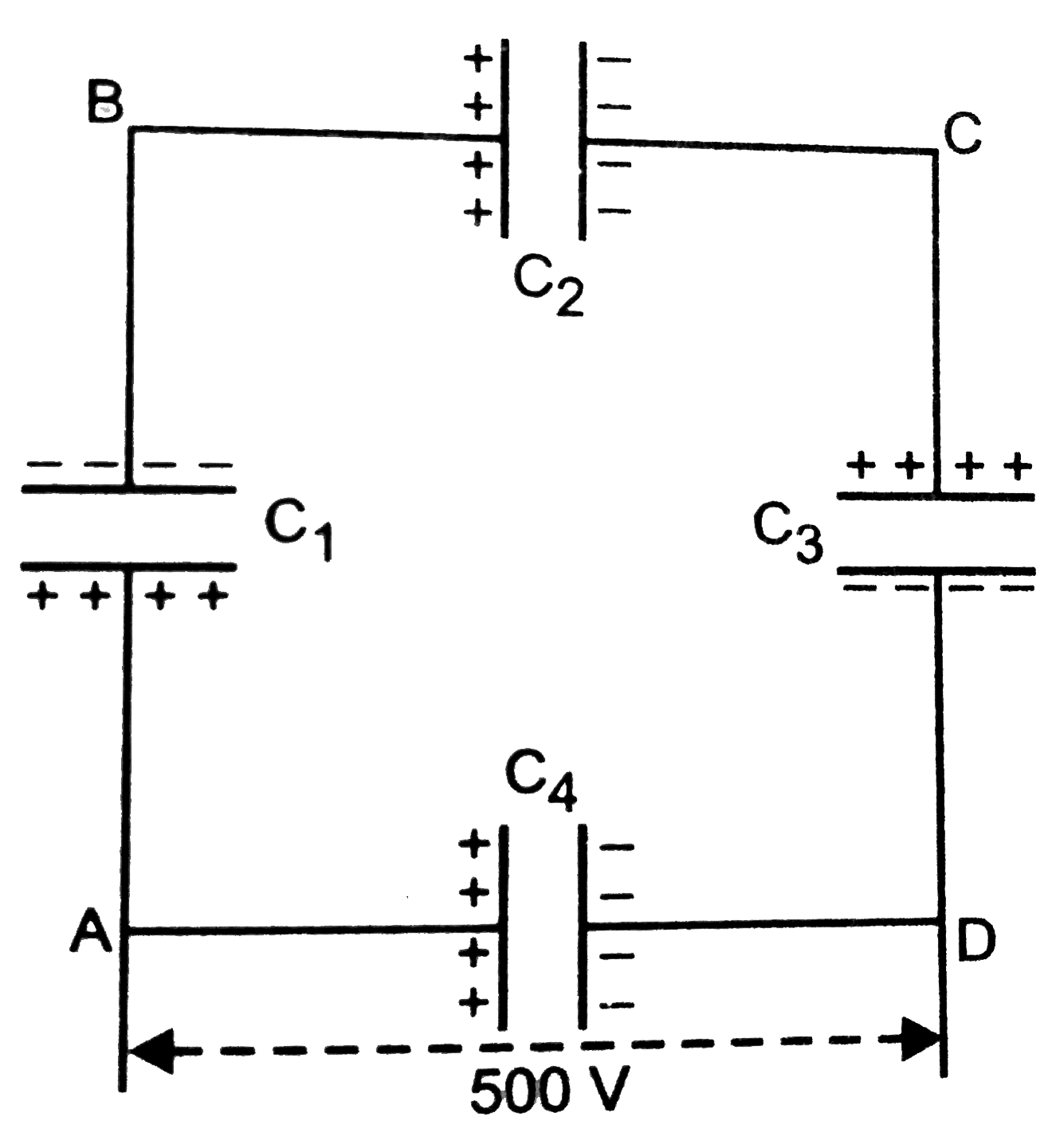
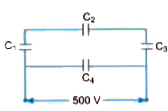
A network of 4 capacitors, each of 6μF is connected to a 240 V supply as shown in the figure. What are the charges on the capacitor C2andC4 ?
View SolutionA network of four 20 μF capacitors is connected to a 600 V supply as shown in the figure.
The equivalent capacitance of the network is

View SolutionA network of four capacitors each of 12 μF capacitance is connected to a 500 V supply as shown in the Fig .
Determine equivalent capacitance of the network .
View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

View SolutionThree capacitors of capacitances 2pF,3pFand4pF are connected in parallel. Determine the charge on each capacitor, if the combination is connected to a 100 V suppy ?
View SolutionTwo capacitors C1 and C2 are connected to a battery of 6V as shown in Fig. Find the charge on each capacitor.
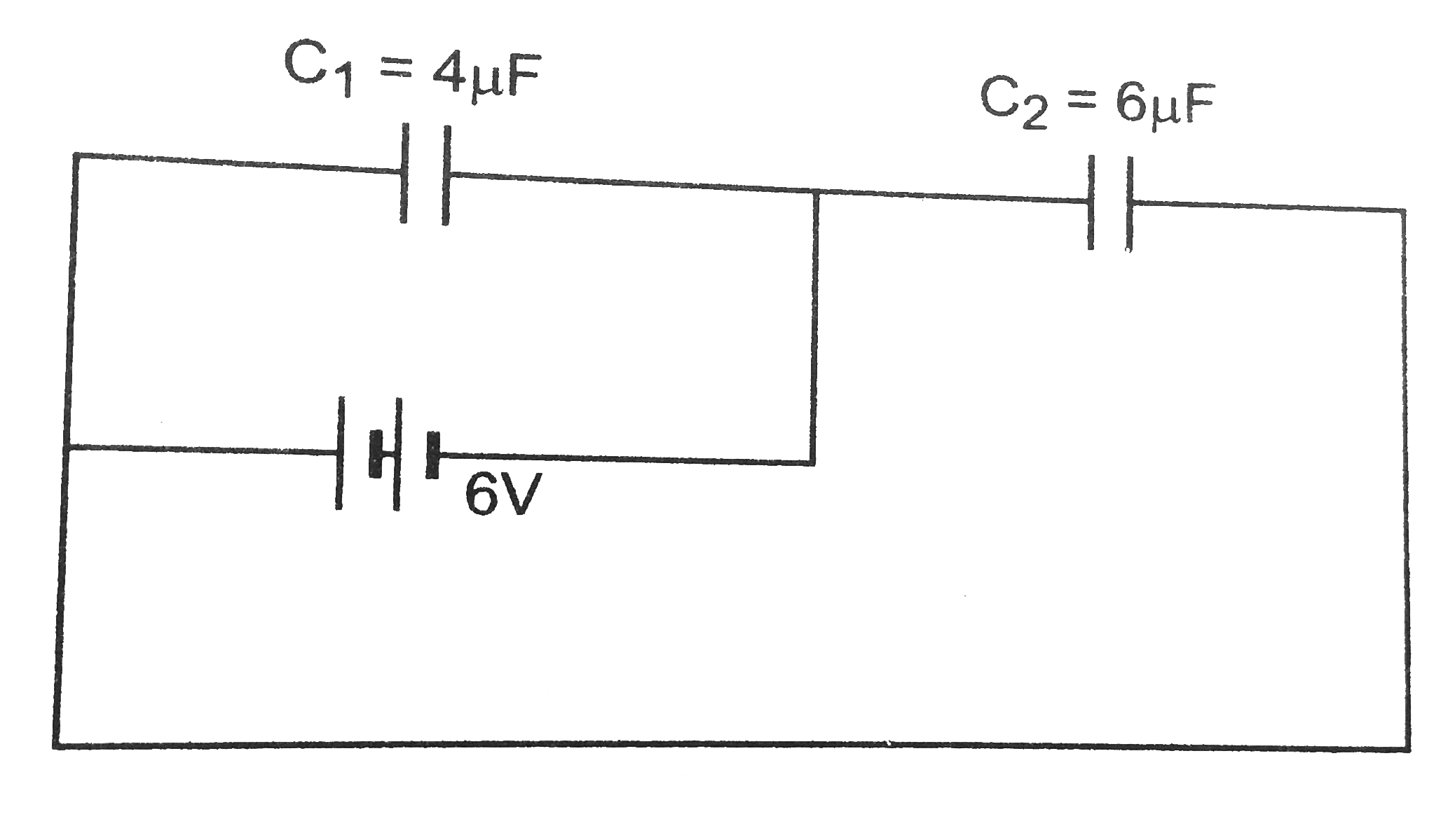
View SolutionA 60 μF capacitor is connected to a 110 V, 60 Hz a.c. supply. Determine the rms value of the current in the circuit.
View Solution
