A thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is

E along OK
E along KO
3E along OK
3E along KO
The correct Answer is:A
Positive charge Q is uniformly distributed over the ring and hence electric field intensity at the centre due to it is zero due to cancellation of fields from diametrically opposite ring. Line OK divides portion AB in two equal parts so from symmetry we know that electric field at point O due to AKB will be directed away from K towards O. To make the net electric field intensity zero at the centre, electric field due to ACDB will be equal and opposite to that due to AKB. Hence, the field due to ACDB will also be E but will be directed from O to K.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (BA.MCQ))
Explore 3 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (BB.MCQ))
Explore 22 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (A.MCQ) )
Explore 56 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
Knowledge Check
A thin conducting ring orf radius R is given a chareg +Q, Fig. The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on part ACDB of the ring is
 A3E along KOBE along OKCE along KOD3E along OK
A3E along KOBE along OKCE along KOD3E along OKA thin conducting ring of radius R is given a charge +Q. The electric field at the centre O of the ring due to the charge on the part ABCD of the ring is
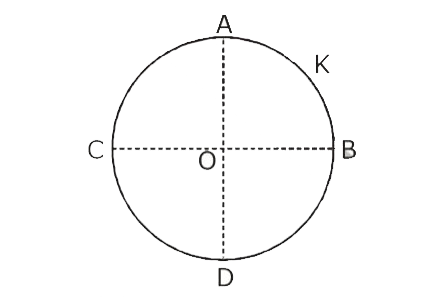 A3E along KOBE along OKCE along KOD3 E along OK
A3E along KOBE along OKCE along KOD3 E along OKCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2
Find the electric field at the centre of a semicircular ring if it is uniformly positive charged.
View SolutionThe electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
View SolutionA conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
View SolutionA small element l cut from a circular ring of radius a and λ charge per unit length. The net electric field at the centre of ring is
View SolutionA fixed ring of radius R is given a charge q. A charge q0 is brought slowly from infinity to the centre of the ring. The wrong statement is-
View Solution

