What is the flux through a cube of side 'a' if a point charge of q is at one of its corner?
q2ε0
2qε0
Q8ε0
qε0
The correct Answer is:C
To find the electric flux through a cube of side 'a' when a point charge 'q' is located at one of its corners, we can apply Gauss's Law. Here is a step-by-step solution:
Step 1: Understand Gauss's Law
Gauss's Law states that the electric flux (Φ) through a closed surface is equal to the charge (Q_enc) enclosed by that surface divided by the permittivity of free space (ε₀):
Φ=Qencε0
Step 2: Analyze the Charge Location
In this case, the charge 'q' is located at one corner of the cube. Since the charge is at the corner, it is not fully enclosed within the cube.
Step 3: Enclose the Charge
To properly apply Gauss's Law, we can imagine a larger cube that fully encloses the charge 'q'. This larger cube can be visualized as being composed of 8 smaller cubes, each identical to the original cube of side 'a'.
Step 4: Calculate the Charge Enclosed
Since the charge 'q' is at one corner of the larger cube, it is shared among the 8 smaller cubes. Therefore, the charge enclosed by one of the smaller cubes is:
Qenc=q8
Step 5: Apply Gauss's Law
Now, we can substitute the enclosed charge into Gauss's Law:
Φ=Qencε0=q/8ε0=q8ε0
Step 6: Conclusion
Thus, the electric flux through the cube of side 'a' with the point charge 'q' at one of its corners is:
Φ=q8ε0
Gauss's Law states that the electric flux (Φ) through a closed surface is equal to the charge (Q_enc) enclosed by that surface divided by the permittivity of free space (ε₀):
Φ=Qencε0
In this case, the charge 'q' is located at one corner of the cube. Since the charge is at the corner, it is not fully enclosed within the cube.
To properly apply Gauss's Law, we can imagine a larger cube that fully encloses the charge 'q'. This larger cube can be visualized as being composed of 8 smaller cubes, each identical to the original cube of side 'a'.
Since the charge 'q' is at one corner of the larger cube, it is shared among the 8 smaller cubes. Therefore, the charge enclosed by one of the smaller cubes is:
Qenc=q8
Now, we can substitute the enclosed charge into Gauss's Law:
Φ=Qencε0=q/8ε0=q8ε0
Thus, the electric flux through the cube of side 'a' with the point charge 'q' at one of its corners is:
Φ=q8ε0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (BA.MCQ))
Explore 3 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (BB.MCQ))
Explore 22 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (A.MCQ) )
Explore 56 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
The total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is
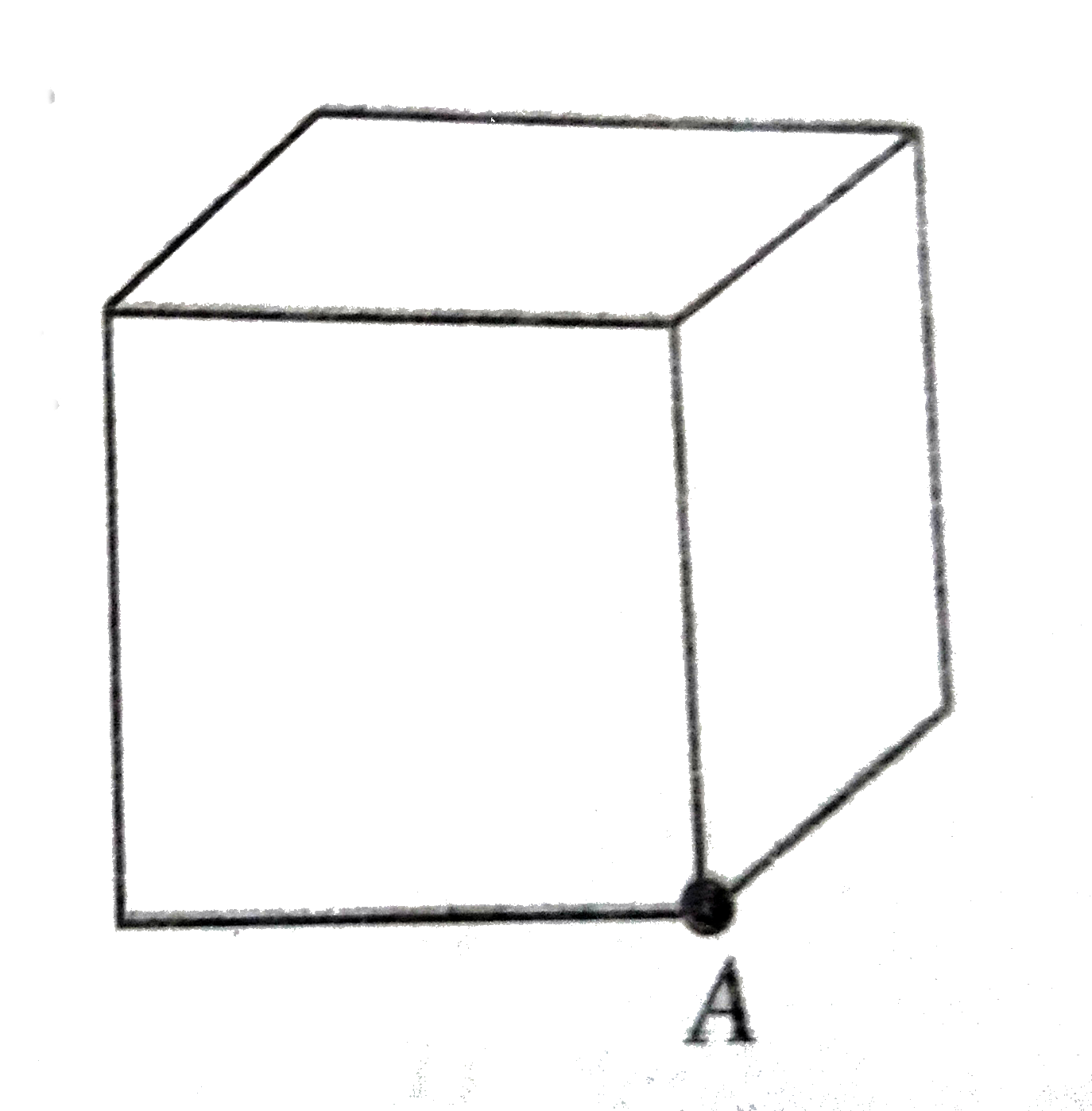
View SolutionIn figure, a charge q is placed at a distance δ→0 near one of the corners of a cube of edge I on a line of symmetry along diagonal.

1. What is the flux through each of the faces containing the point a?
2. What is the flux through the other three faces?
View Solution
Knowledge Check
What is the flux link through a cube of side l if a charge 2q is placed at one end of cube ?
Aqε0Bq8ε0C2qε0Dq4ε0A point charge q is kept at a corner of a cube
AElectric flux linked with individual faces of the cube may be zeroBElectric flux linked with individual faces of the cube may be non-zeroCElectric flux linked with a certain face of the cube may be q/8ε0DElectric flux linked with a certain face of the cube may be q/24ε0The total electric flux through a cube when a charge 8q is placed at one corner of the cube is
Aε0qBε0qCqε0Dq4πε0
Eight equal point charges each of charge 'q' and mass 'm' are placed at eight corners of a cube of side 'a'
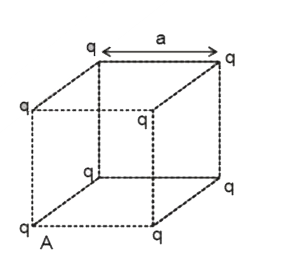
If keeping all other charges fix, charge of corner 'A' is released then find out its speed when it is at infinite distance ?
View SolutionThe total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is

View SolutionThe total electric flux through a cube when a charge 8q is placed at one comer of the cube is
View SolutionElectric flux through a cube with charge q inside is
View SolutionA point charge q is placed at a distance a2 directly above the centre of a horizontal square of side 'a' and another point charge -q is placed at a distance 'a' directly below one of its (the square's) corners. The electric flux through the square is :
View Solution

