A thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
θ=tan−1(p1+p2p1−p2
θ=tan−1(p1−p2p1+p2)
θ=tan−1(p2p1)
θ=tan−1(p1p2)
The correct Answer is:B
Let r be the radius of the ciruclar tube
Let PA=PC=P0

PB=P0+P1(r−rsinθ)g.......(i)
PB=P0+p2(rsinθ+rcosθ)g+p1(r−rcosθ)g.......(ii)
Equation (i) and (ii)
p1(r−rsinθ)=p2(rsinθ+rcosθ)+p1(r−rcosθ)
p1(r−rsinθ−r+rcosθ)=p2(rsinθ+rcosθ)
p1(rcosθ−rsinθ)=p2(rsinθ+rcosθ)
p1p2=sinθ+cosθcosθ−sinθ=tanθ+11−tanθ
p1−p1tanθ=p2+p2tanθ
(p1+p2)tanθ=p1−p2
θ=tan−1(p1−p2p1+p2)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (JEE (Advanced) For IIT Entrance)
Explore 14 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (C. MCQ With More Than One Correct Answers)
Explore 12 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
Explore 6 Videos
- MATHEMATICAL TOOLSBook:MODERN PUBLICATIONChapter:MATHEMATICAL TOOLSExercise:PRACTICE PROBLEMS (10)
Explore 12 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
Similar Questions
Knowledge Check
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
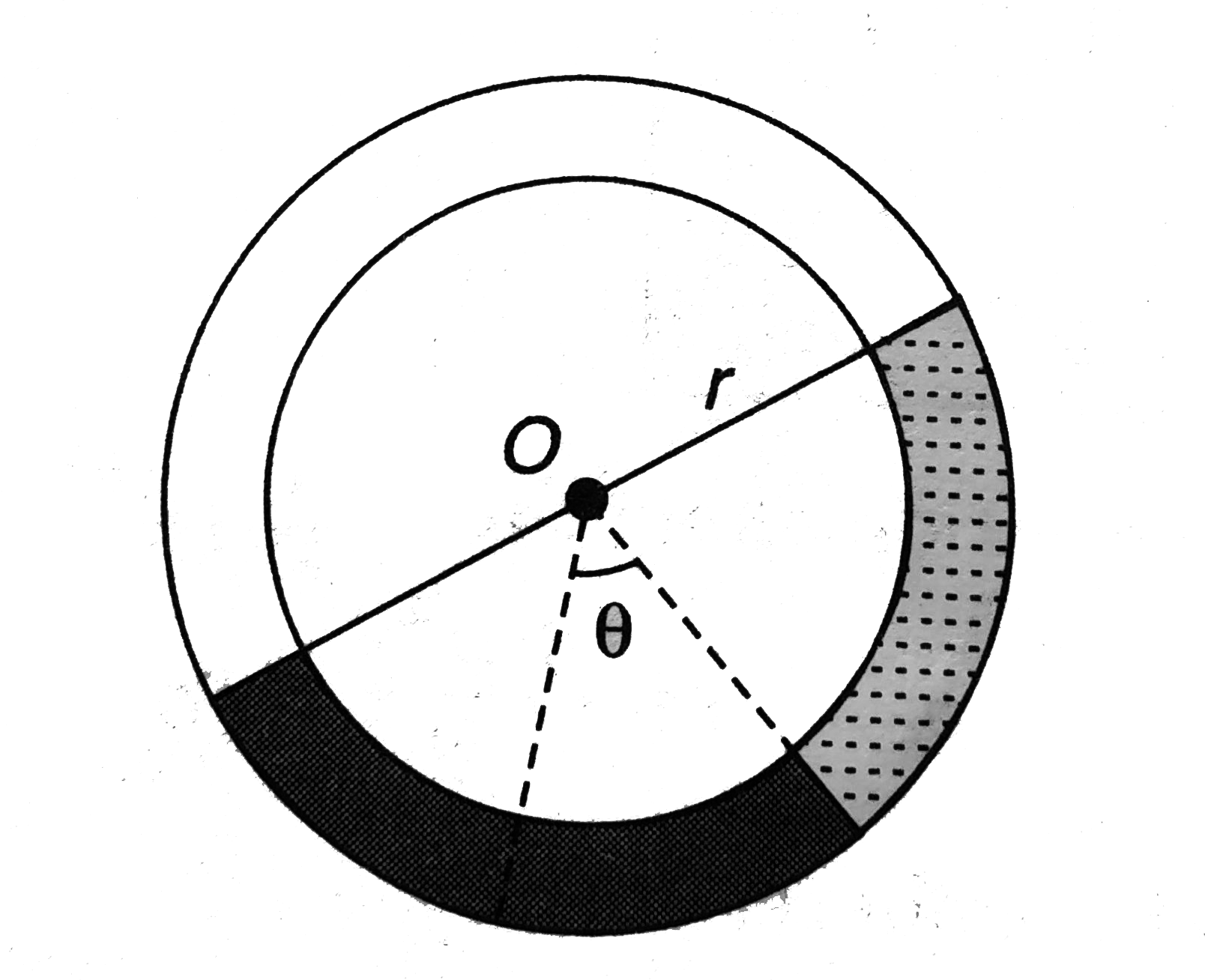 Atan−1(ρ+σρ−σ)Btan−1(ρ−σρ−σ)Ctan−1(ρ+σρ+σ)Dtan−1(ρ−σρ+σ)
Atan−1(ρ+σρ−σ)Btan−1(ρ−σρ−σ)Ctan−1(ρ+σρ+σ)Dtan−1(ρ−σρ+σ)A thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to
 A√3−12−√3B√3+12+√3C√3−1√3+1D√3+1√3−1
A√3−12−√3B√3+12+√3C√3−1√3+1D√3+1√3−1A uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
 Atan−1(ρ−δρ+δ)Btan−1(ρδ)Ctan−1(δρ)Dtan−1(ρ+δρ−δ)
Atan−1(ρ−δρ+δ)Btan−1(ρδ)Ctan−1(δρ)Dtan−1(ρ+δρ−δ)
A solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
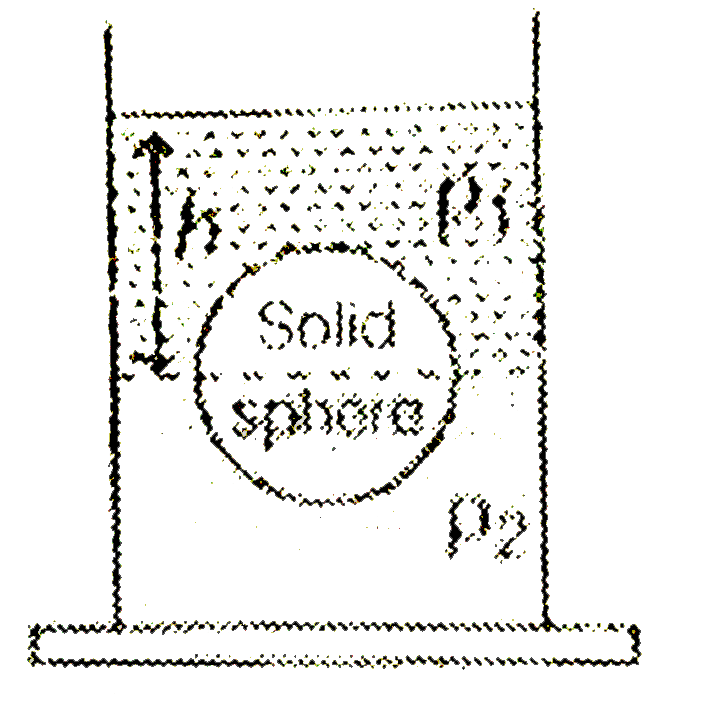
View SolutionTwo circular discs A and B have equal masses and uniform thickness but have densities ρ1 and ρ2 such that ρ1>ρ2 . Their moments of inertia is
View SolutionTwo disc has same mass rotates about the same axis with their densities ρ1 and ρ2 respectively such that (ρ1>ρ2), then the relation between I1 and I2 will be
View SolutionThree liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View Solution


