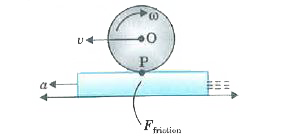
Consider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is $F_{friction}$ at point P? It is assumed that the cylinder does not slip.

A

$M g$

B

$M a$

C

$\frac{M a}{2}$

D

$\frac{M a}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Force of friction acting at point P,
$F_{friction} = \frac{1}{3} M a sin θ$
$= \frac{1}{3} M a {sin 90}^{\circ} [here θ = 90^{\circ}]$
$= \frac{M a}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is $I_{1}$ and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is $I_{2}$
A $l_{2} - l_{1} = M R^{2}$
B $l_{2} = l_{1}$
C $\frac{l_{2}}{l_{1}} = \frac{19}{12}$
D $l_{1} - l_{2} = M R^{2}$
Question 2 - Select One
The moment of inertia of a solid cylinder of mass M, length 2 R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I, and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is $I_{2}$ then
A $I_{2} > I_{1}$
B $I_{2} - I_{1} = M R^{2}$
C $\frac{I_{2}}{I_{1}} = \frac{19}{12}$
D $\frac{I_{2}}{I_{1}} = \frac{7}{6}$
Question 3 - Select One

A uniform solid cylinder of mass $m$ and radius $R$ is placed on a rough horizontal surface. A horizontal constant force $F$ is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
A $F / 3 m$
B $2 F / 3 m$
C $4 F / 3 m$
D $5 F / 3 m$

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )

Home
Ask Doubt
Profile