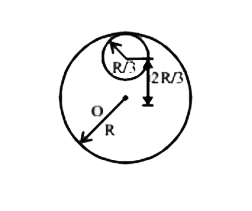
A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
219MR2256
237MR2512
19MR2512
197MR2256
The correct Answer is:B
Moment of inertia along the axis passing through centre of mass and perpendicular to the plane of full disc having radius R about .O. point
Itotal=MR22
Radius of removed disc =R/4
Mass of removed dics =MR2πR2×π(R4)2=M/16
Moment of inertia of removed disc about its own axis O. is
Icm=12M16(R4)2=MR2512
Moment of inertia of removed disc about O point
Iremoved disc=Icm+M16x2
[using parallel axis theorem]
=MR2512+M16(3R4)2=19MR2512
Moment of inertia of remaining disc
Iremaining disc=Itotal−Iremoved disc=MR22−19MR2512
=237512MR2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
Explore 35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
Explore 10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
Explore 67 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A circular of radius R has mass 9m . A hole of radius R3 is cut from it as shown in figure. The moment of inertia of the remaining part about an axis passing through centre 0 of the disc and perpendicular of the plane of disc is xmR2 .Find value of x
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution
Knowledge Check
The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A(MR2B32MR[^(2)CMR22D54MR2If a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
Amoment of inertia decreasesBmoment of inertia increasesCradius of gyration increasesDradius of gyration decreasesThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correct
A circular hole of radius r/2 is cut from a circular disc of radius 'r'. The disc lies in the xy plane. Determine the moment of inertia about an axis passing through the centre and perpendicular to the plane of the disc.
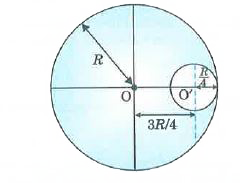
View SolutionA uniform disc having radius 2R and mass density σ as shown in figure. If a small disc of radius R is cut from the disc as shown. Then find out the moment of inertia of remaining disc around the axis that passes through O and is perpendicular to the plane of the page.
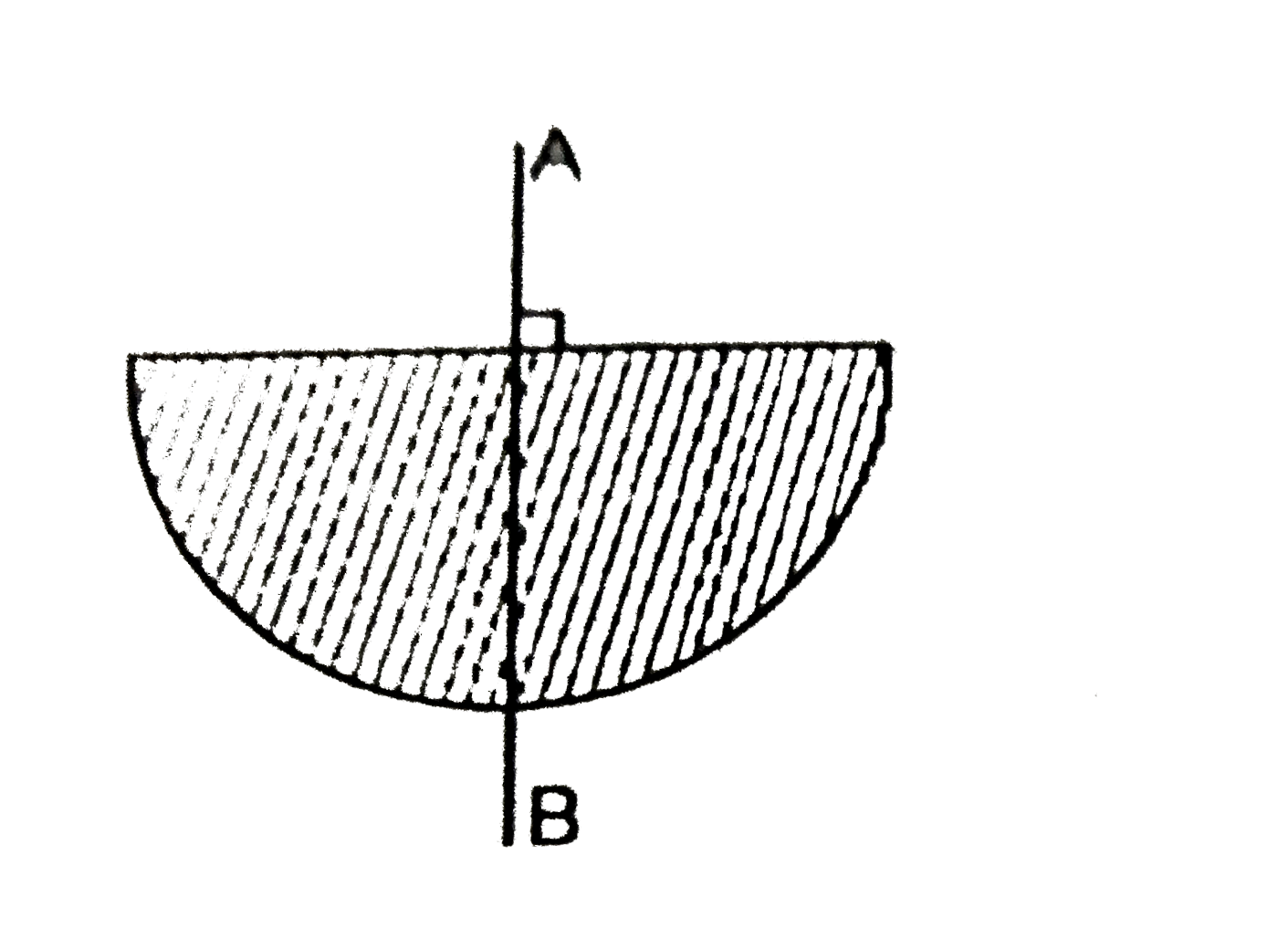
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
View Solution

