A circular hole of radius is cut from a circular disc of radius . The disc lies in the plane. Determine the moment of inertia about an axis passing through the centre and perpendicular to the plane of the disc.
Step by step video & image solution for A circular hole of radius r//2 is cut from a circular disc of radius 'r'. The disc lies in the xy plane. Determine the moment of inertia about an axis passing through the centre and perpendicular to the plane of the disc. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE83videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
A disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A(MR2B32MR[^(2)CMR22D54MR2 - Question 2 - Select One
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correct - Question 3 - Select One
From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
 A56MR2B53MR2C512MR2D524MR2
A56MR2B53MR2C512MR2D524MR2
A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
 View Solution
View SolutionA circular hole of radius R/2 is cut from a circular disc of radius R. The disc lies in the xy-plane and its centre coincides with the origin. If the remaining mass of the disc is M, then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the z-axis.
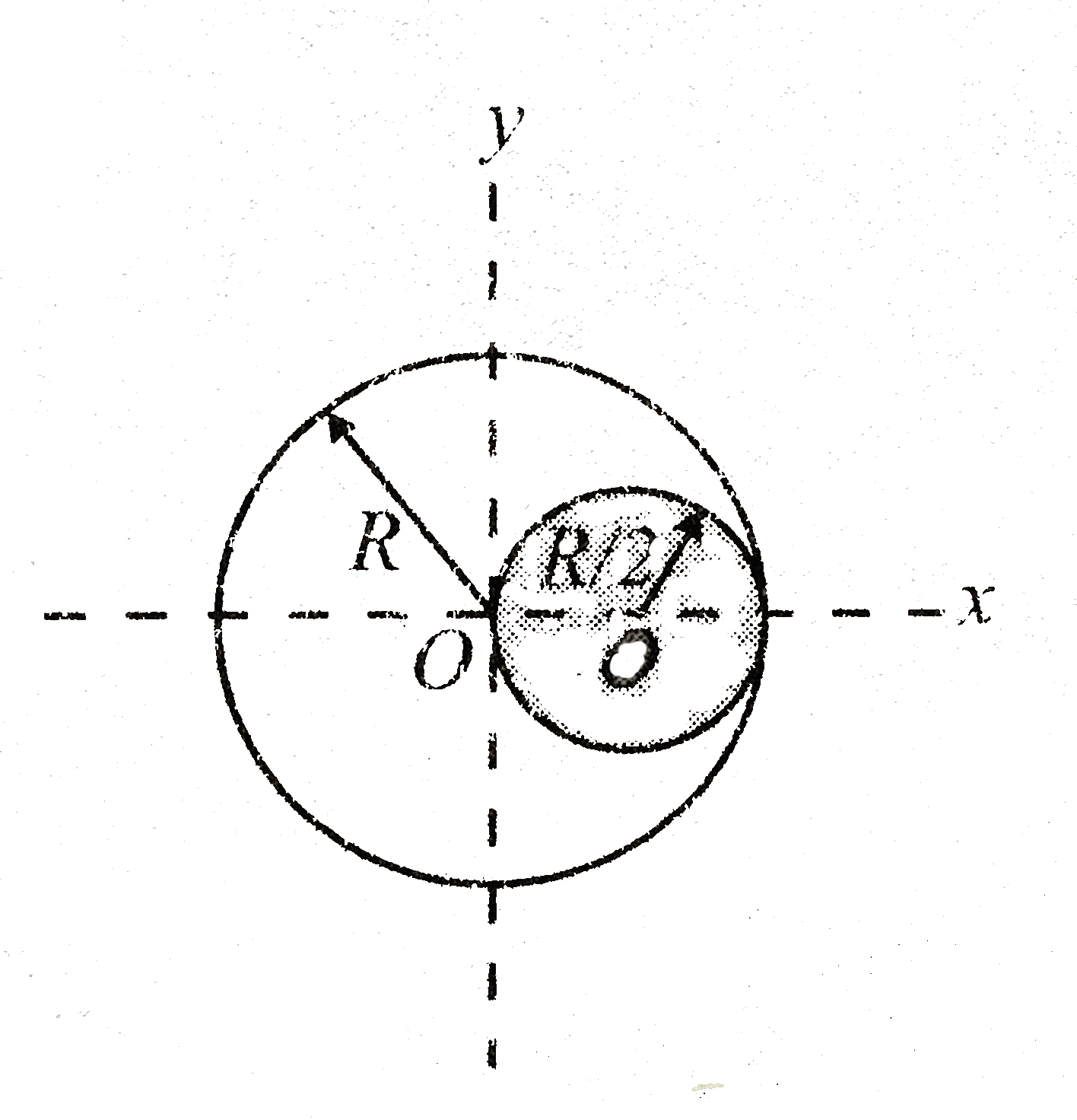 View Solution
View SolutionA circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is (about an axis passing through centre and perpendicular to the disc)
View SolutionOne circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
View Solution

