A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as $k {(\frac{x}{L})}^{n}$ where n can be zero or any positive number. If the position $X_{C M}$ of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of $X_{C M}$ on n?

A

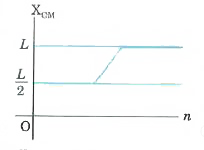
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$X_{c m} = \frac{\int x d m}{\int d m} = \frac{\int x ρ A d x}{\int ρ A d x} = \frac{\int_{0}^{L} x k \frac{x^{n}}{L^{n}} d x}{\int_{0}^{L} k \frac{x^{n}}{L^{n}} d x}$
$= \frac{k {[\frac{x^{n + 2}}{(n + 2) L^{n}}]}_{0}^{L}}{k {[\frac{x^{n + 1}}{(n + 1) L^{n}}]}_{0}^{L}} = L (\frac{n + 1}{n + 2})$

If n=0,1,2,3,4,5,…
then $X_{c m} = \frac{L}{2}, \frac{2 L}{3}, \frac{3 L}{4}, \frac{4 L}{5}, \frac{5 L}{6}$
As n increases, the centre of mass shifts towards the end x = L

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as $k {(\frac{x}{L})}^{n}$ where n can be zero or any positive integer. If position $X_{c m}$ of centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of $x_{C M}$ on n?
A
B
C
D
Question 2 - Select One
A thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as $k x^{4}$ . Find the position of centre of mass of rod in meters.
A5m
B3m
C2m
D4m

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )

Home
Ask Doubt
Profile