A small particle of mass is projected at an angle with the - axis with an initial velocity in the plane as shown in the figure . At a time , the angular momentum of the particle is
where are unit vectors along - axis respectively.
The correct Answer is:D
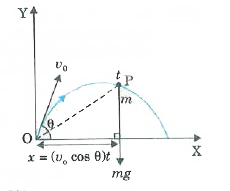
Let the particle reach at point Pin time t. Horizontal distance travelled by particle is which is perpendicular to the line of action of force acting on the particle as shown in figure,
Torque acting about .O. is:
Torque = force perpendicular distance of line of action of force
Also,
For motion of the particle in X-Y plane, is along
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
67 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A small particle of mass m is projected at an angle θ with x-axis with initial velocity υ0 in x-y plane as shown in Fig. Calculate the momentum of the particle
at t<υ0sinθg.

View SolutionA small particle of mass m is projected at an angle θ with the x-axis, with initial velocity v0 in the x-y plane. Just before time 2v0sinθg , the angular momentum of the particle about the point of projection is
View Solution
Knowledge Check
The angle which the vector →A=2ˆi+3ˆj makes with the y-axis, where ˆi and ˆj are unit vectors along x- and y-axis, respectively, is
Acos−1(3/5)Bcos−1(2/3)Ctan^(-1)(2//3)Dsin−1(2/3)The angle θ between the vector →p=ˆi+ˆj+ˆk and unit vector along X-axis is
Acos−1(1√3)Bcos−1(1√2)Ccos−1(√32)Dcos−1(12)If θ is the angle between the vectors 4(ˆi−ˆk)andˆi+ˆj+ˆk, then what is (sinθ+cosθ) equal to ?
A0B12C1D2
A particle moves in x-y plane according to the equation ¯r=(ˆi+2ˆj)Acosωt the motion of the particle is
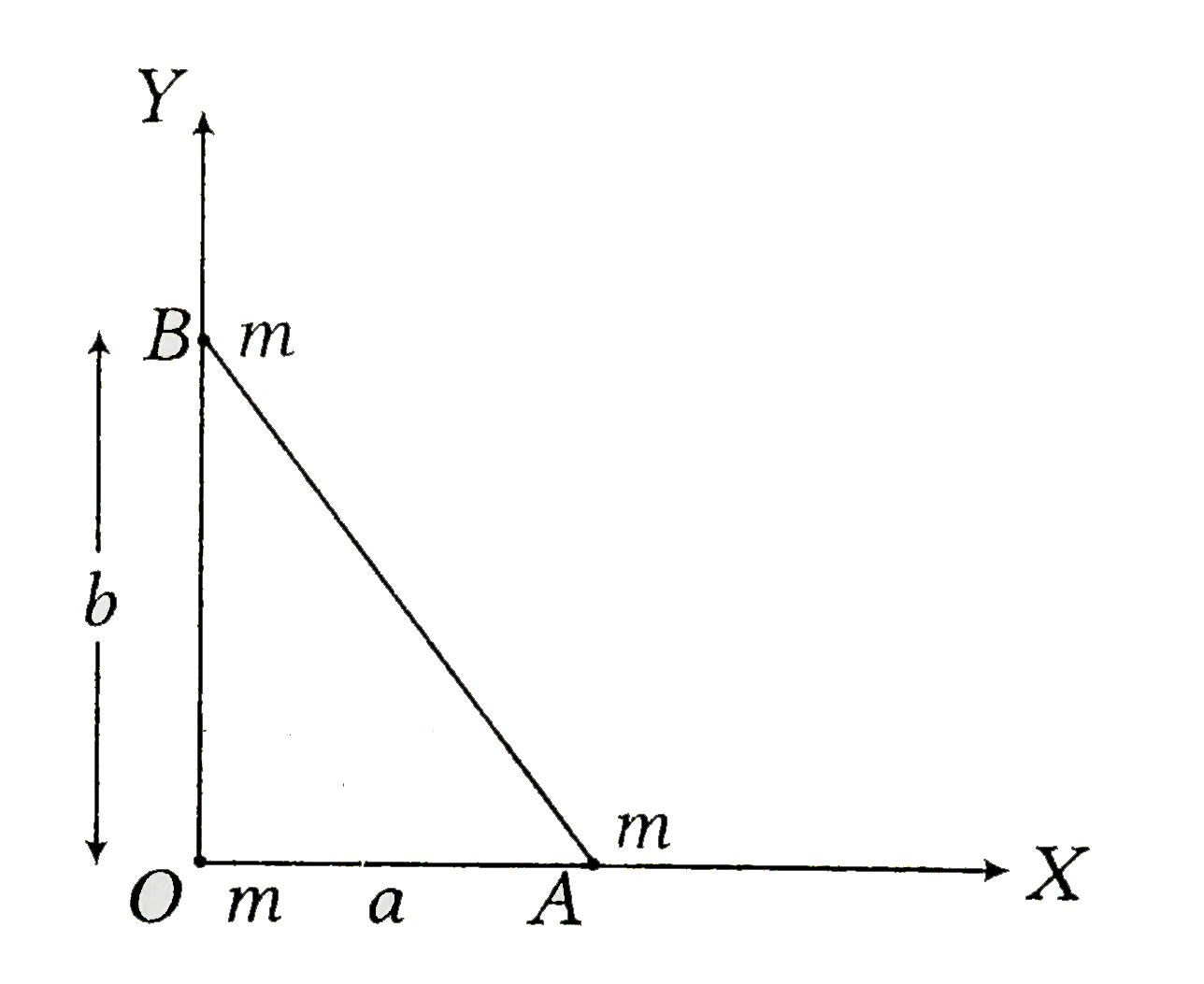
View SolutionThree particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and ˆi,ˆj,ˆk are unit vectors)
View SolutionThe unit mass having r=8ˆi−4ˆjandv=8ˆi+4ˆj in its angular momentum is
View SolutionA particle of mass m moves in the xy-plane with velocity of →v=vxˆi+vyˆj. When its position vector is →r=x→i+y→j, the angular momentum of the particle about the origin is.
View SolutionA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:

View Solution
