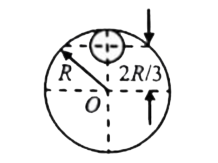
A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
10MR2
379MR2
4MR2
409MR2
The correct Answer is:C
Volume of the cut portion is 1/9 of total volume of disc, hence mass of the cut portion is M, because total mass given is 9M.
We can find moment of inertia of disc without hole about the given axis through centre and then subtract moment of inertia of smaller disc (which is cut through) about the centre of bigger disc.
I=(9M)R22−(M2(R3)2+M(2R3)2)
Note that moment of inertia of smaller disc is written using parallel axis theorem. Solving the above expression we get,
I=4MR2
Hence option (c) is correct.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
Explore 35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
Explore 10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
Explore 67 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A thin disc of mass 9M and radius R is given.Now a disc of radius (R/3) is cut as shown in figure.The new position of C .m from orgin will be :-
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of mass M and radius R3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
View Solution
Knowledge Check
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
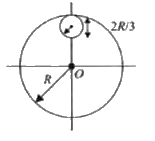 A4M2B409MR2C10MR2D379MR2
A4M2B409MR2C10MR2D379MR2Form a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
AMR2B4MR2C49MR2D409MR2
Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
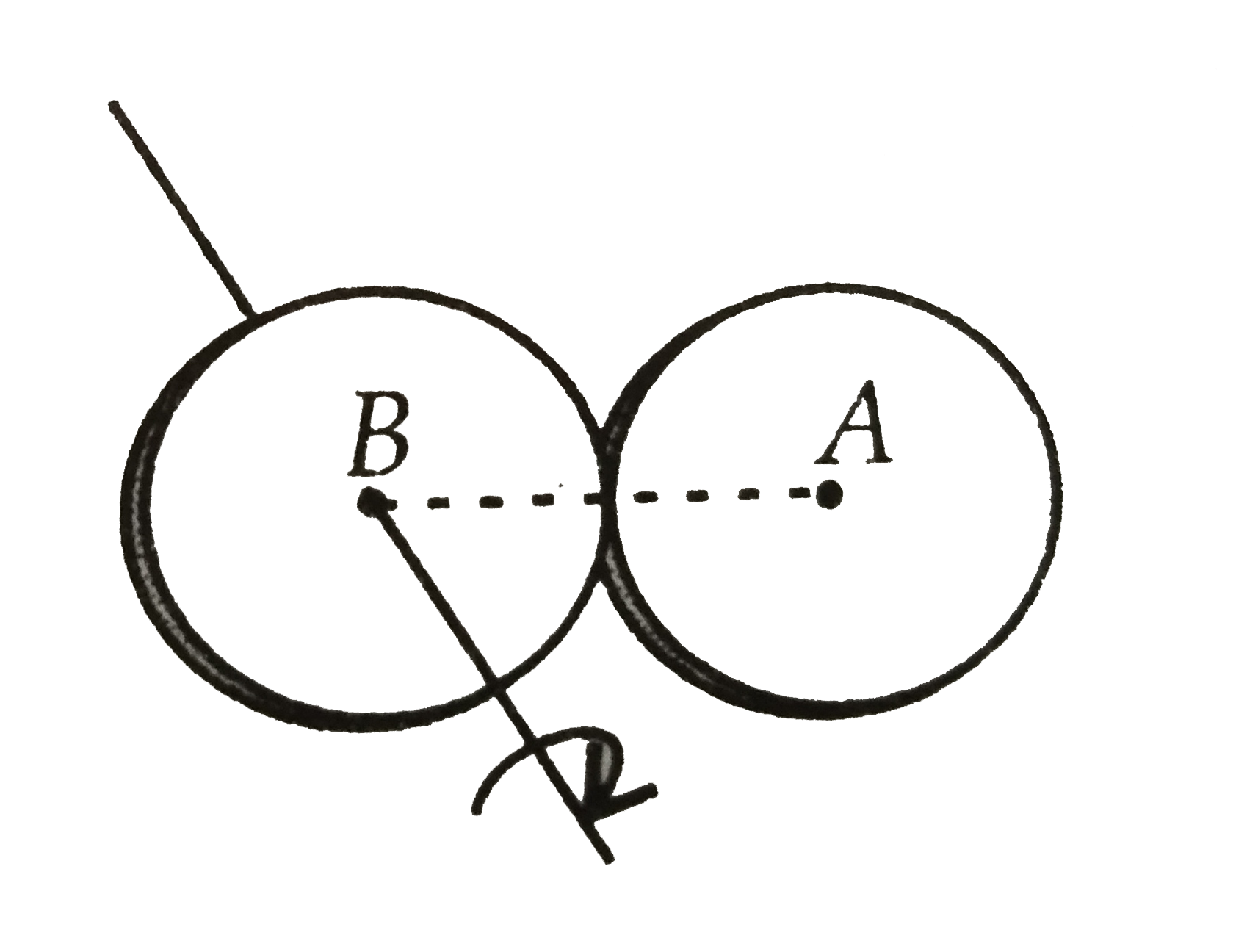
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View SolutionFrom a disc of mass 2kg and radius 4m a small disc of radius 1 m with center O' is extracted . The new moment of inertia,about an axis passing through O perpendicular to plane of disc is

View SolutionTwo thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
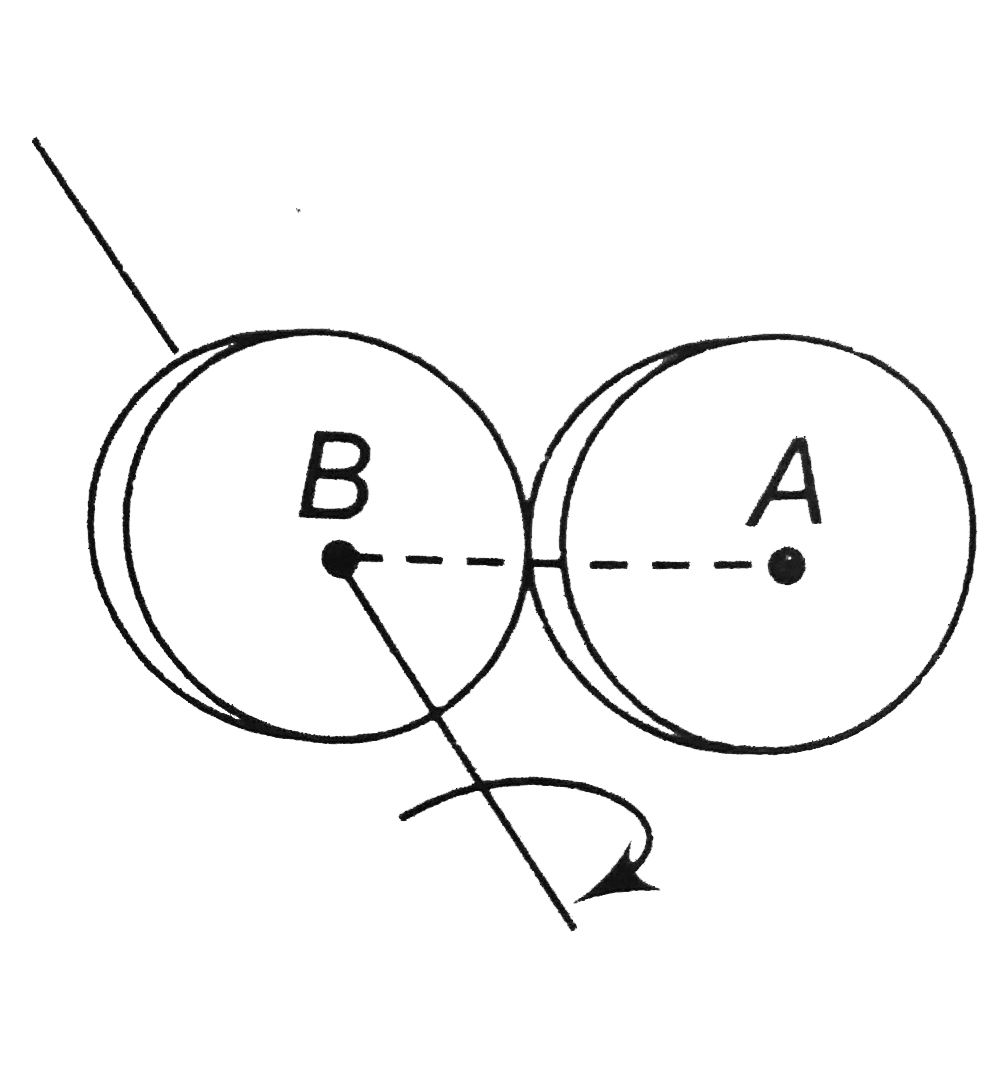 .
.
View SolutionA rectangular piece of dimension l×b is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :
View Solution

