Let P denotes a complex number z=r(cosθ+isinθ) on the Argand's plane, and Q denotes a complex number √2|z|2(cos(θ+π4)+isin(θ+π4)). If 'O' is the origin, then ΔOPQ is
A
isosceles but not right angled
B
right angled but not isosceles
C
right isosceles
D
equilateral
Video Solution
Text Solution
The correct Answer is:C
(c) 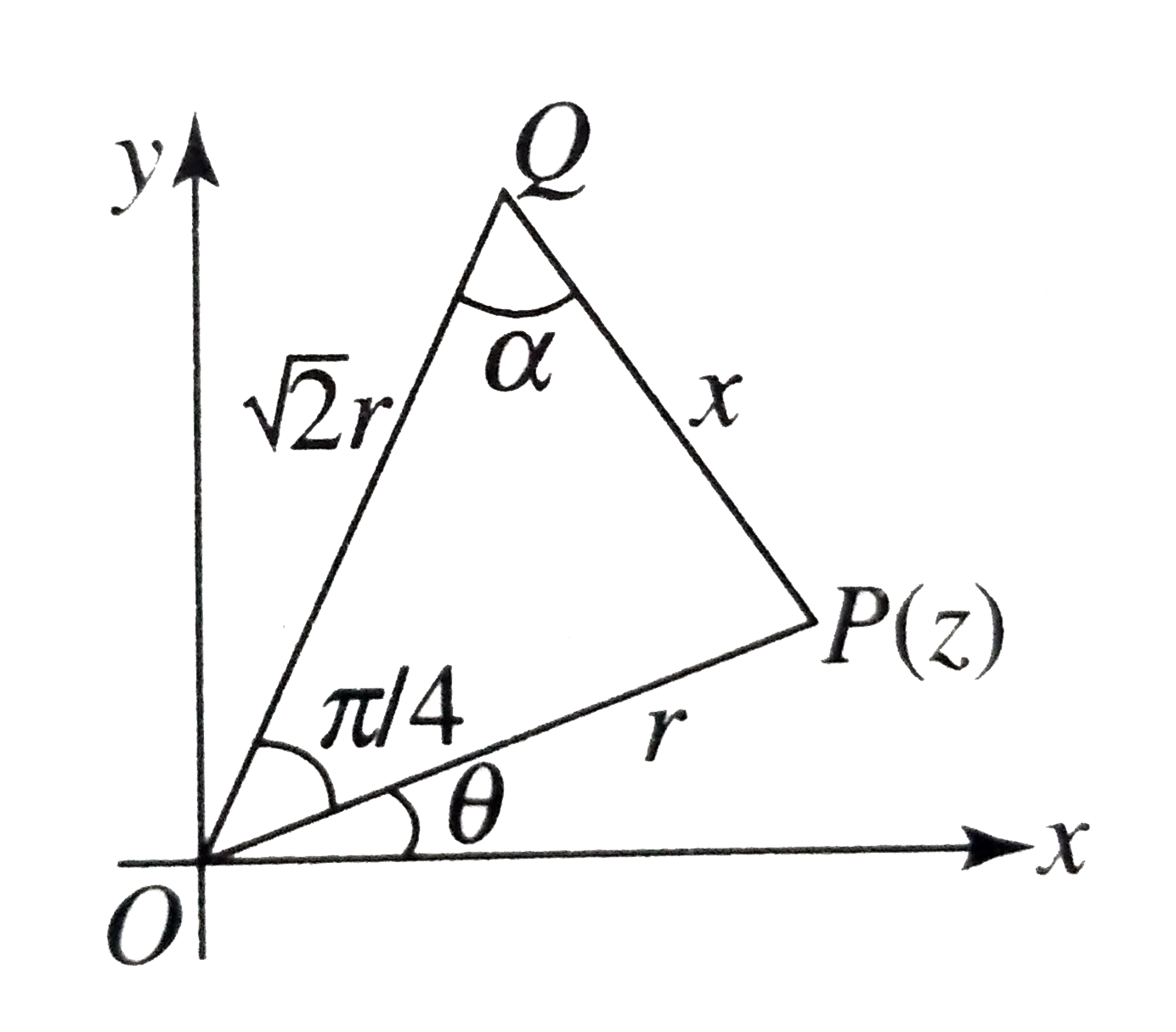
ZP=r(cosθ+isinθ)
Z0=√2|z|2(cos(θ+π4)+isin(θ+π4))
=√2r[cos(θ+π4)+isin(θ+π4)]
From the figure,
cosπ4=2r2+r2−x22⋅√2r⋅r=3r2−x22√2r2
∴1=3r2−x22r2
⇒r2=x2⇒x=r⇒ Triangle is right isosceles.
|
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Video
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
91 Videos
Similar Questions
Knowledge Check
The argument of the complex number z=(1+i√3)(1+i)(cosθ+isinθ)is7π2+θ
Aπ3+θBπ4+θC7π12+θDnoneThe modulus of the complex number z=(1−i√3)(cosθ+isinθ)2(1−i)(cosθ−isinθ) is
A1√2B12√2C1√3DNone of theseIf z≠0 be a complex number and arg(z)=π/4, then
ARe(z)=Im(z) onlyBRe(z)=Im(z)>0CRe(z2)=Im(z2)Dnone of these
If z is a complex number such taht z2=(¯z)2, then find the location of z on the Argand plane.
View SolutionGiven that |z−a|=a, and |b−a|=|b−2a|=a where z is a point in the Argand's plane, then the complex number b can be
View Solution∫π/2π/4cosθ(cos θ2+sin θ2) dθ
View SolutionExpress the complex number in the form r(cosθ+isinθ)
(ii)1−sinα+icosα
View SolutionIf z is a complex number, then amp (z−1z+1)=π2 will be
View Solution