Let z∈C and if A={z:arg(z)=π4}and B={z:arg(z−3−3i)=2π3}. Then n(A⌢B)=
A
1
B
2
C
3
D
0
Video Solution
Text Solution
The correct Answer is:D
(d) A={z,arg(z)=π4}
z lies on the ray from origin (excluding origin) at an angle π/4 with positive real axis.
B={z,arg(z−3−3i)=2π3}
z lies on the ray from 3+3i(excluding 3+3i) at an angle 2π/3 with positive real axis.
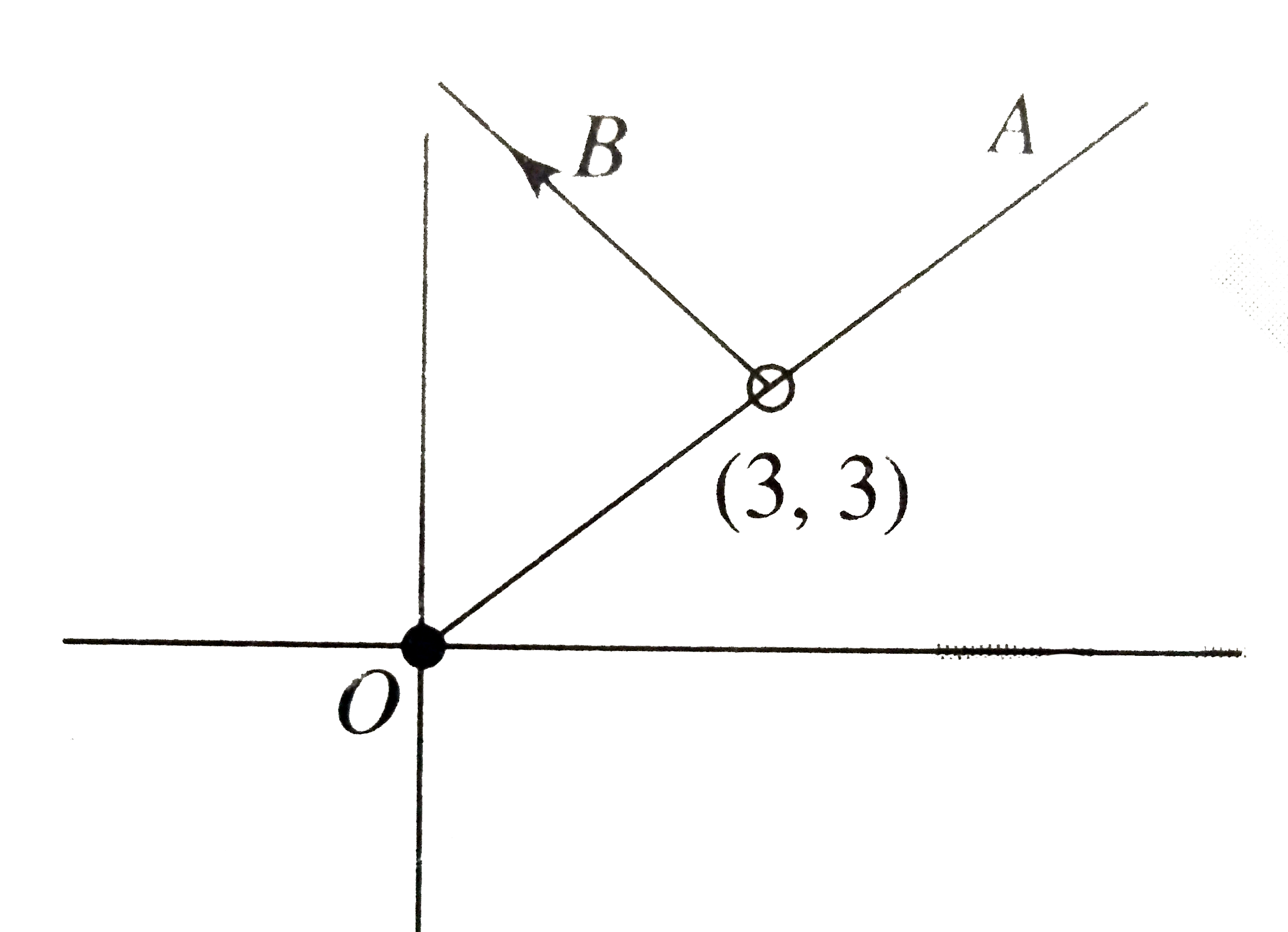
We can observe that 3+3i∈A but ≠B
∴n(A∩B)=0
|
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
91 Videos
Similar Questions
Knowledge Check
If arg(z+a)=π6 and arg(z−a)=2π3(a∈R+), then
A|z|=aB|z|=2aCarg(z)=π3Darg(z)=π2If arg(z+a)=π/6andarg(z−a)=2π/3(a∈R+), then
A|z|=aB|z|=2aCarg(z)=π2Darg(z)=π3If arg z=π/4
ARez2=Imz2BImz2=0CRez2=0Dnone of these
