Let $O$ , $A$ , $B$ be three collinear points such that $O A . O B = 1$ . If $O$ and $B$ represent the complex numbers $O$ and $z$ , then $A$ represents

A

$\frac{1}{¯ z}$

B

$\frac{1}{z}$

C

$¯ z$

D

$z^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$(a)$ Let $A$ represents $z_{1}$ .
Since $O A . O B = 1 ∴ | z_{1} - 0 | . | z - 0 | = 1$
$\Rightarrow | z_{2} | = \frac{1}{| z |}$
Also, $a r g (\frac{z_{1} - 0}{z - 0}) = 0 \Rightarrow a r g (\frac{z_{1}}{z}) = 0$
$\Rightarrow a r g z_{1} = a r g z$
If $θ$ is the argument of $z$ , then
$z = | z | e^{i θ}$
$∴ z_{1} = \frac{1}{| z |} e^{e θ} = \frac{1}{{| z |}^{2}} | z | e^{i θ} - \frac{z}{z ¯ z} = \frac{1}{¯ z}$
$∴ A$ is $\frac{1}{¯ a z}$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let OP.OQ=1 and let O,P and Q be three collinear points. If O and Q represent the complex numbers of origin and z respectively, then P represents
A $\frac{1}{z}$
B $¯ z$
C $\frac{1}{¯ z}$
D $- z$
Question 2 - Select One
Let A,B,C be three collinear points which are such that AB.AC=1 and the points are represented in the Argand plane by the complex numbers, 0, $z_{1}$ and $z_{2}$ respectively. Then,
A $z_{1} z_{2} = 1$
B $z_{1} {¯ z}_{2} = 1$
C $| z_{1} | | z_{2} | = 1$
D $z_{1} = {¯ z}_{2} ∣$
Question 3 - Select One
In a given parallelogram, if the points $P_{1}$ and $P_{2}$ represent two complex numbers $z_{1}$ and $z_{2}$ , then the point $P_{3}$ represents the number
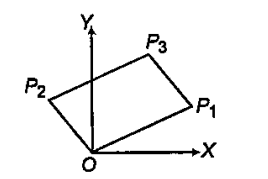A $z_{1} + z_{2}$
B $z_{1} - z_{2}$
C $z_{1} \times z_{2}$
D $z_{1} + z_{2}$

CENGAGE-COMPLEX NUMBERS-Single correct Answer

Home
Ask Doubt
Profile