Find the coordination of the centre of mass of a uniform semicircular wire of radius R and mass M.
Video Solution
Text Solution

Figure shows a uniform semicircular wire of radius r and mass M . Its centre O is taken as the origin , the line joining its ends as x - axis in the plane of the wire is taken as y - axis
Let us take radius making an angle θ with the x - axis . Now consider a small element of length edthη of the wire . Its coordinates are (rcosθ,rsinθ)
Its mass dmMπr=Mπr.rdθ=Mπdθ
The centre of mass lies on the axis of symmetry .
The coordinate of the centre of mass are
XCM=0
YCM=1M∫ydm=1M01∫0(rsinθ)Mπdθ
=rπ[−cosθ]π0=2rπ
Hence the centre of mass is (0,2rπ)
|
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EVALUATE YOURSELF - 1
Explore 9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EVALUATE YOURSELF - 4
Explore 11 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
Knowledge Check
Find the coordinates of centre of mass of a uniform semicircular closed wire frame with respect to the origin which is at its centre. Radius of the circular portion is R
 A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)
A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
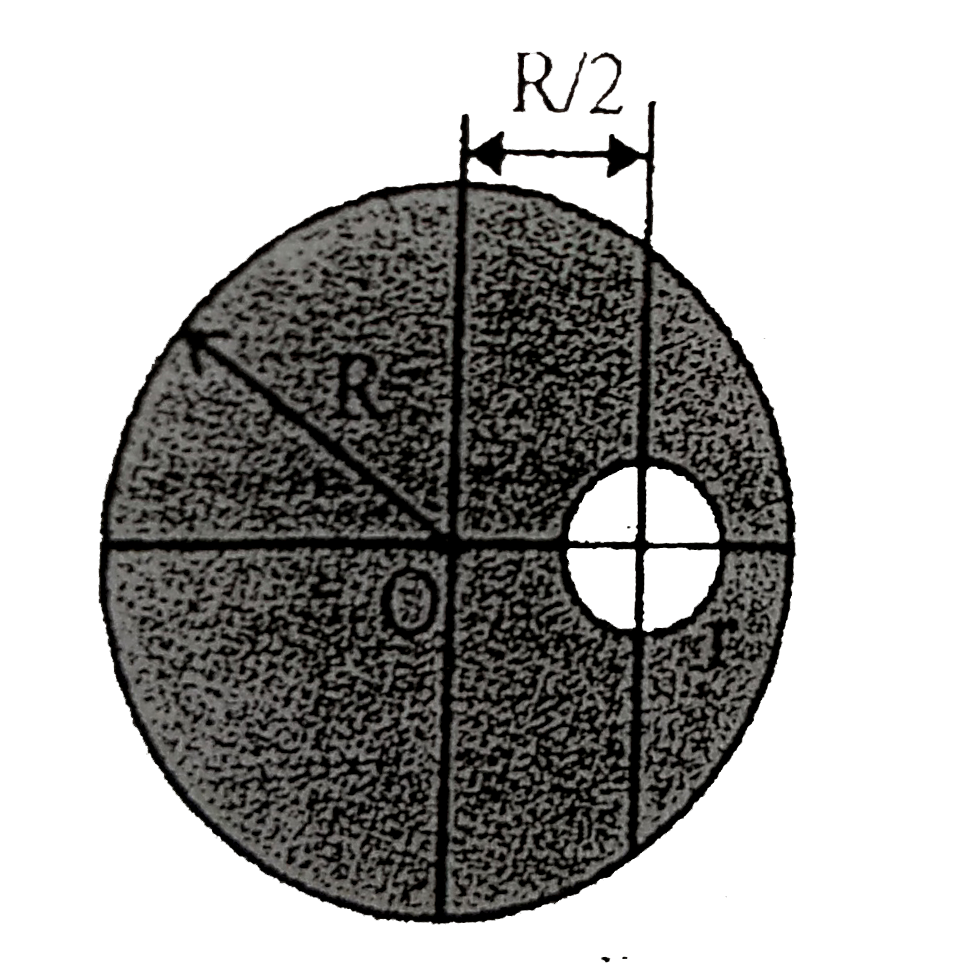 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
Locate c.m. of thin , uniform semicircular wire of radius R.
View SolutionFind the centre of mass of a homogeneous semicircular plate of radius a.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionFind the centre of mass of a uniform solid cone.
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View Solution
