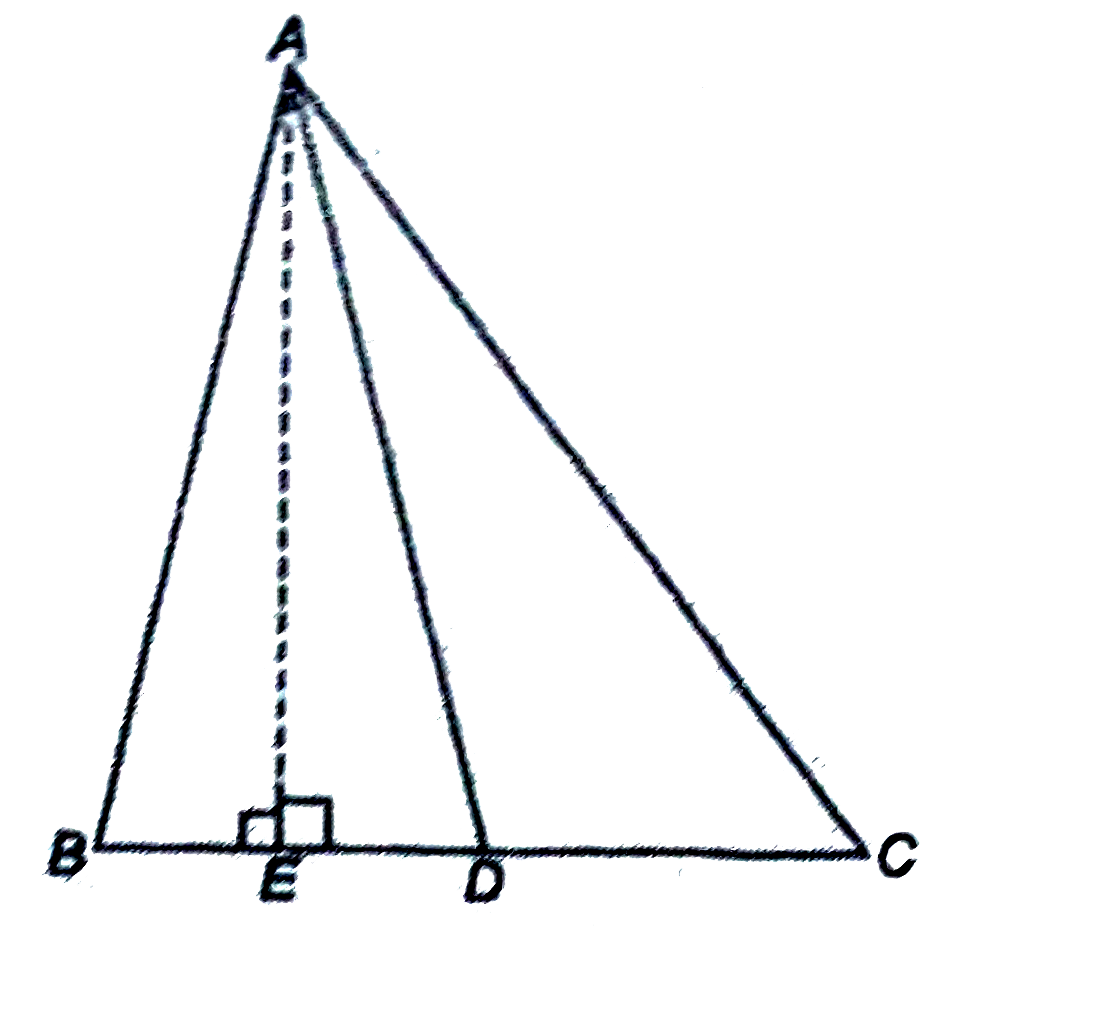
In a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
△ABC in which AD is the median , i.e. BD= DC = BC2
To prove : AB2+AC2=2AD2+12BC2
Construction: Draw AE⊥BC
Proof : L.H.S. = AB2+AC2
(AE2+BE2)+(AE2+EC2)
(by Pythagores theorem)
2AE2+BE2+EC2
2(AD2−DE2)+BD−ED)2)+(ED+DC)2
2AD2−2DE2+BD2+ED2−2BD.ED+ED2+DC2+2ED.DC
=2D2+(12BC)2−2BC2.ED+(12BC)2+2ED(BC2) (DB=DC=BC2
=2AD2+12BC2
R.H.S. Hence proved
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
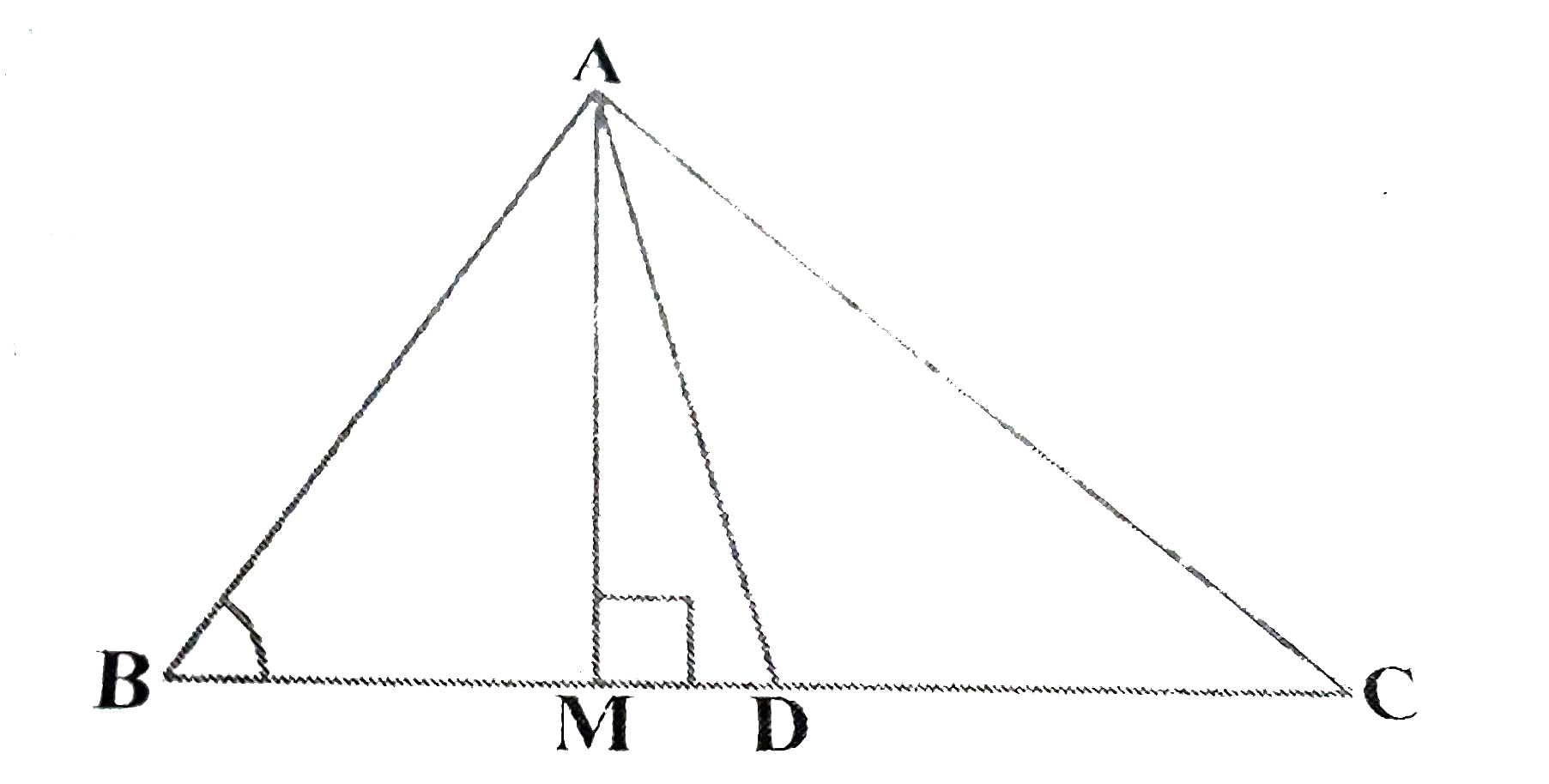
In figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
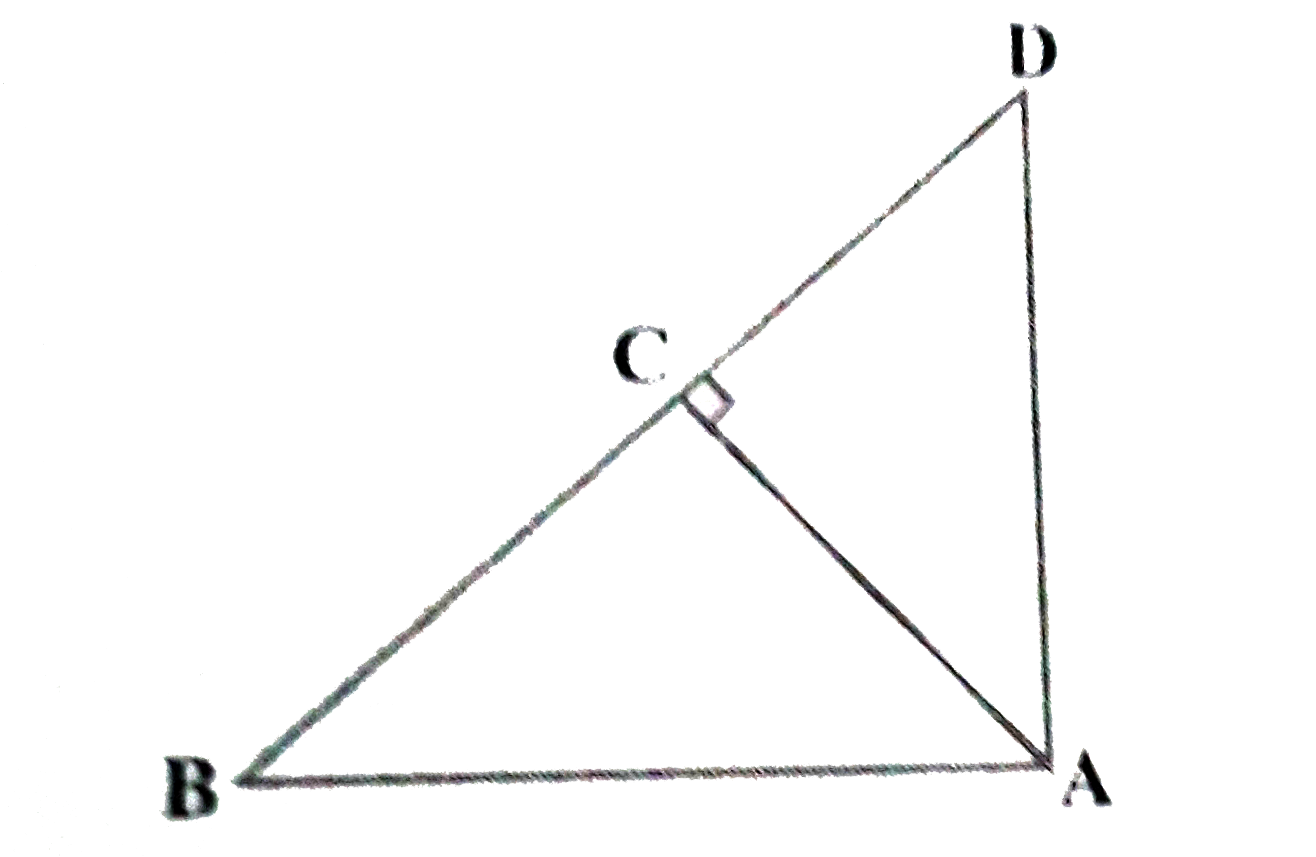
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

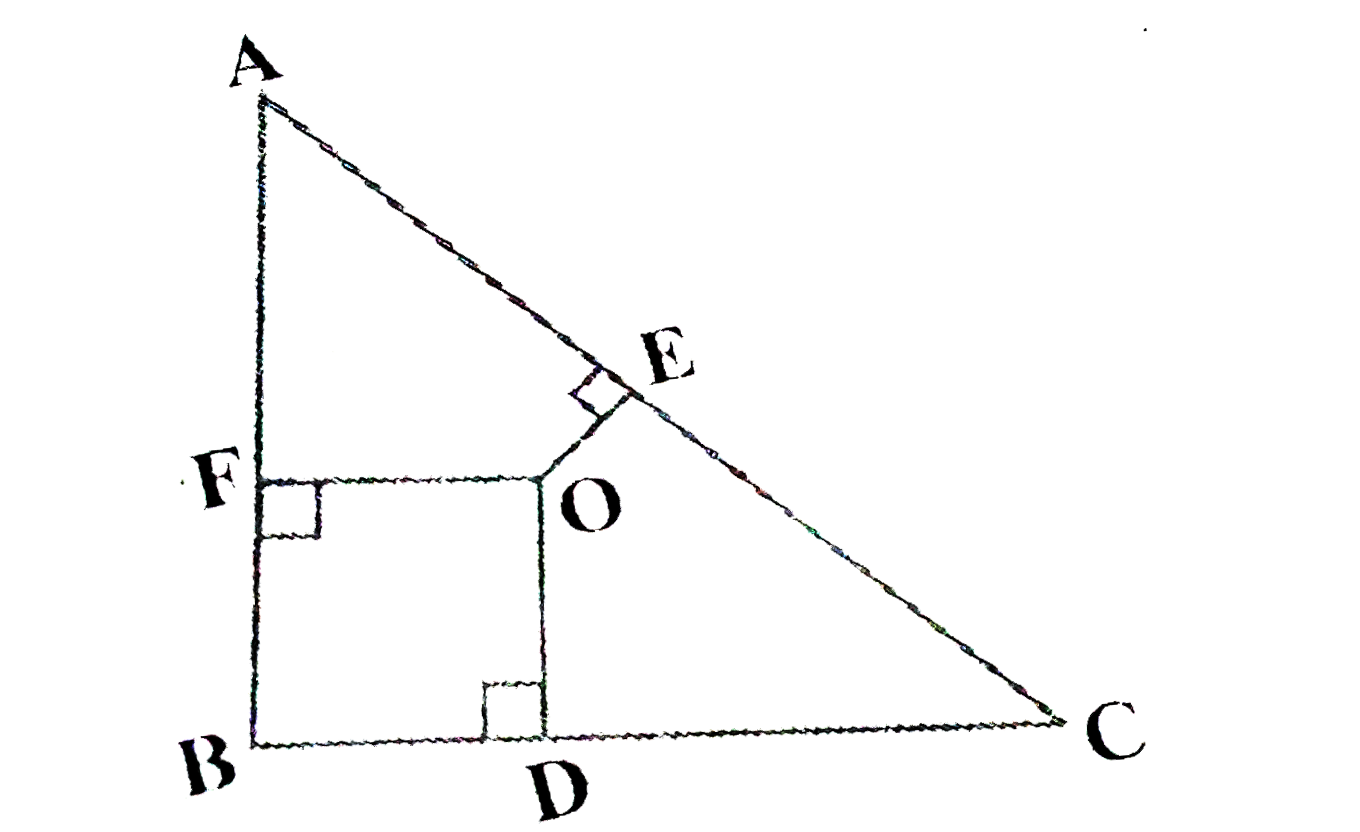
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionABCD is a parallelogram and E is the mid-point of BC, DE and AB when produced meet at F. Then AF= 32AB (b) 2 AB (c) 3 AB (c) 54 AB
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View Solution