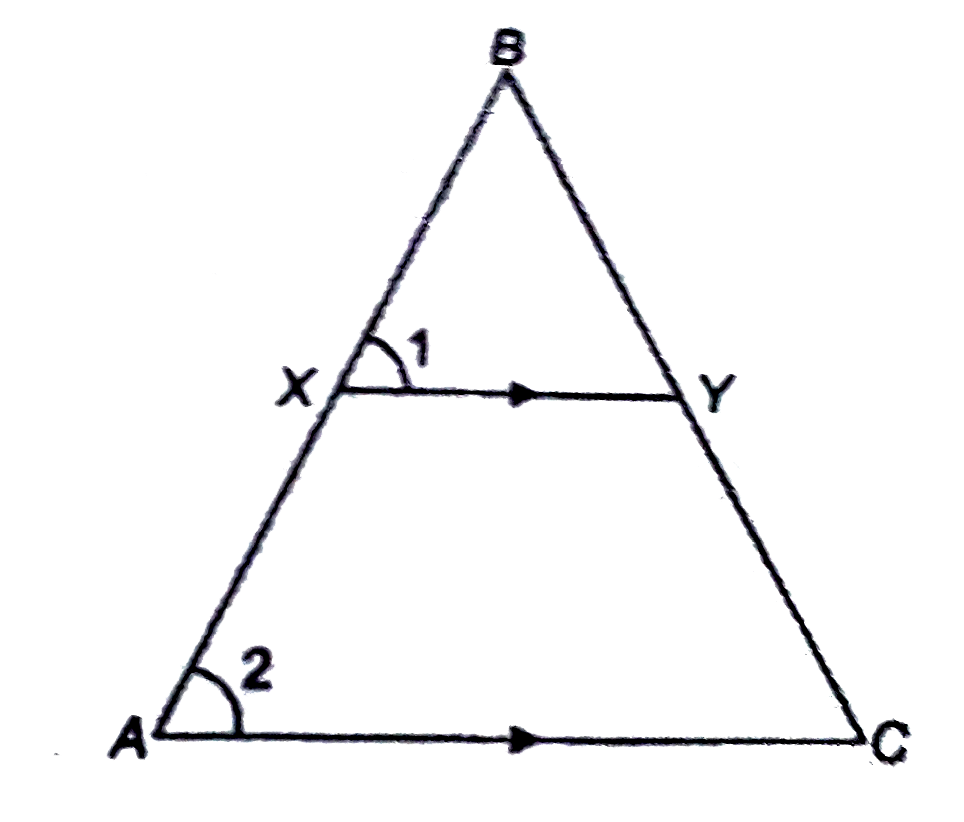
X and Y are points on the sides AB and BC respectively of △ABC such that XY||AC and XY divides △ABC into two parts in area , find AXAB
Video Solution
Text Solution
Since XY||AC
In△BXYand△BAC.
∠1=∠2 (corresponding angles)
∠B=∠B (common)
△BXY~△BAC (AA corollary)
ar(△BXY)ar(△BAC)=BX2BA2 (area ratio theorem) ....(1)
But ar(△BXY)=12ar(△ABC) (given)
⇒ ar(△BXY)ar(△ABC)=12
from (1) and (2) we get
BX2AB2=12⇒BXAB1√2
⇒ AB−AXAB=1√2⇒ABAB−AXAB=1√2
⇒ 1−AXAB=1√2⇒AXAB=1−1√2=√2−1√2
Hence , AXAB=2−√22
|
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In △ABC, F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD⊥BC and AD intersect FE at G, then GD: AG = ?
△ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD⊥BC है और AD, FE को G पर काटती है, तो GD: AG = ?A√2:1B(√2−1):1C2√2:1D(√2+1):1In ΔABC, D and E are points on AB and AC respectively such that DE||BC and DE divides the ΔABC into two parts of equal areas. Then ratio of AD and BD is
A1:1B1:√2−1C1:√2D1:√2+1X and Y are points on sides AB and AC respectively of ΔABC. For which of the following cases will XY be parallel to BC?
AAX = 1.3 cm, XB = 3.9 cm,
AY = 2.8 cm, YC = 5.6 cm,BAX = 1.3 cm, XB = 3.9 cm,
AY = 2.8 cm, YC = 8.4 cmCAX = 1.3 cm, XB = 2.6 cm,
AY = 2.8 cm, YC = 8.4 cmDAX = 1.3 cm, XB = 2.6 cm,
AY = 2.8 cm, YC = 11.2 cm
If P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
View SolutionIn the given figure, XY∣∣ACandXY divides ΔABC into two regions, equal in area. Find the value of AXAB
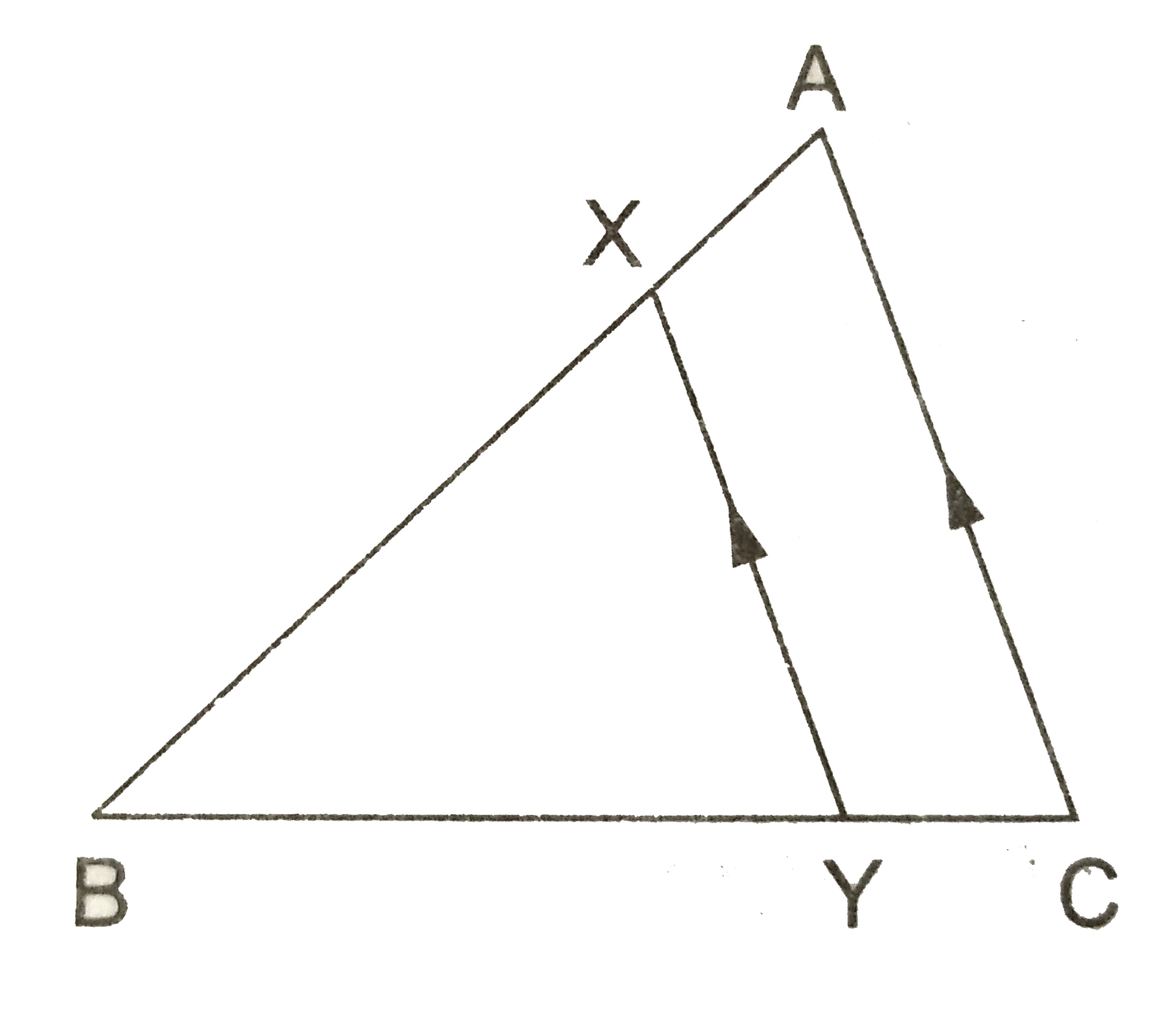
View SolutionP and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionIn Figure, X and Y are two points on equal sides AB and AC of a ABC such that AX=AY. Prove that XC=YB.
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC and O is any point in the plane of △ABC. Show that (1)¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF=¯0
View Solution
