If D,E,F are the mid-points of the sides BC, Ca and AB respectively of a triangle ABC, prove by vector method that Area of $Δ D E F$ = 1/4 Area of $Δ A B C$

Video Solution

Text Solution

Verified by Experts

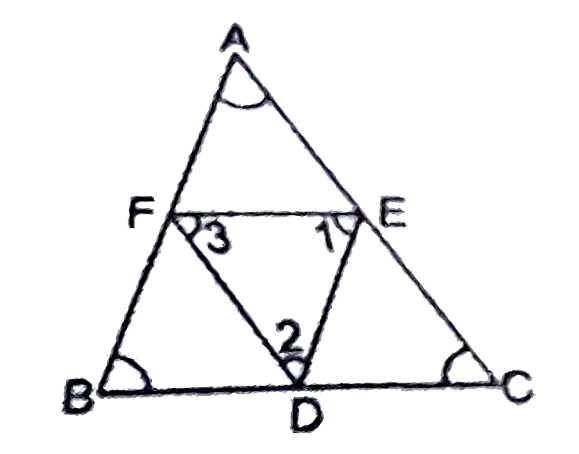
Given: $△ A B C$ in which , D E and F are mid-point if the sides, BC, CA and AB respectively.
To porve: To determine the ratio of the areas of $△ D E F and △ A B C$
proof: Since D,E,F are the mid-point
EF||BC and $E F = \frac{1}{2} B C$
EF=BD
Similarly, DE= BF ( $D E ∣ ∣ A B and \frac{1}{2} A B)$
So, EFBD is a parallelogram.
$∠ B = ∠ 1$
Similarly , AFDE and EFDC and parallelogram
$\Rightarrow ∠ A = ∠ 2 and ∠ C = ∠ 3$
$i . e . △ A B C and △ D E F$ are equiangular
$\Rightarrow △ D E F ~ △ A B C$
$\frac{a r (△ D E F)}{a r (△ A B C)} = \frac{D E^{2}}{(A B^{2})} = \frac{F B^{2}}{A B^{2}} = \frac{{(A B / 2)}^{2}}{A B^{2}} = \frac{1}{4}$
Hence ((ar(triangleDEF))/((ar(trangleABC))= 1/4

Updated on:21/07/2023