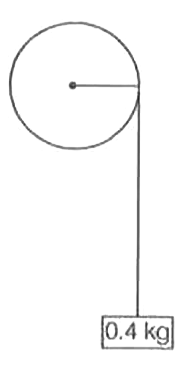
A wheel of radius 8 cm is attached to a support so as to rotate about a horizontal axis through its centre. A string of negligible mass wrapped arounf its circumference carries a mass of 0.4 kg attached to its free end. When the mass is released, it descends through 1m in 10 seconds, then its moment of inertia is (Acceleration due to gravity, g=10ms−2)
 Solution in Telugu
Solution in Telugu
1.277kgm2
2.177kgm2
21.77kgm2
12.77kgm2
The correct Answer is:A
Given, radius of wheel, R=8×10−2m, mass of weight, m=0.4kg, descending length, L = 1 m and time, t = 10 s
As, torque τ=F.R=mgR
putting the given values, we get
=0.4×10×8×10−2
So, τ=0.32Nm
Let the wheel is rotated by an angle θ,
θ=arcradius=10.08=12.5 rad
So, from the equation of rotational motion,
θ=ω0t+αt22
⇒α=2θt2=2×12.510×10=0.25rad s−2
[∵ω0=0]
Now, as
Torque, τ=Iα
∴ Moment of inertia of a wheel,
I=τα=0.320.25=1.28kg−m2
Hence, the correct option is (a).
Topper's Solved these Questions
- QUESTION PAPER 2019Book:TS EAMCET PREVIOUS YEAR PAPERSChapter:QUESTION PAPER 2019Exercise:Physics
Explore 80 Videos
- TS EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER (2018)Book:TS EAMCET PREVIOUS YEAR PAPERSChapter:TS EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER (2018)Exercise:PHYSICS
Explore 40 Videos
Similar Questions
Albert Einstein was confermed with the Nobel prize in physics for his work on
View SolutionChoose the incorrect statement from the following
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA wheel of radius 6cm is mounted so as to rotate about a horizontal axis through its centre. A string of negligibe mass wrapped round its circumference carries a mass of 0.2kg attrached to its free end. When let fall, the mass descends through 1m in 5s. Calculate the angular acceleration of the wheel, its moment of inertia and tension in the cord.
View SolutionFive particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View SolutionA ring of mass 10 kg and diameter 0.4m is rotated about an axis passing through its centre and perpendicular to its plane moment of inertia of the ring is
View SolutionFive particles of mass 2 kg each are attached to the rim of a circular disc of radius 0.1 m and negligible mass. Moment of inertia of the system about the axis passing through the centre of the disc and perpendicular to its plane is
View Solution10 किग्रा द्रव्यमान के एक पहिये का इसकी अक्ष के परितः जड़त्व आघूर्ण 160 किग्रा ”मी”2 है। इसकी घूर्णन त्रिज्या होगी।
View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA wheel of radius 0.4 m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of 8 rad s−2 is produced in it due to the torque. Then moment inergia of the wheel is (g = 10ms−2)
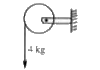
View SolutionFive particles of mass 2 kg each are attached to the rim of a circular disc of radius 0.1 m and negligible mass. Moment of inertia of the system about the axis passing through the centre of the disc and perpendicular to its plane is
View SolutionA wheel of radius 0.4 m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of 8 rad - s−2 is produced in it due to the torque. Then moment inertia of the wheel is (g=10 ms−2)

View SolutionFive particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
View SolutionOne end of a massless string is wound around a cylinder of mass 5 kg and radius 16' cm. The cylinder' is mounted symmetrically on a horizontal axle so 5 that It can freely rotate about its axis, to the other end of the string a mass of 500 gm is attached. Calculate the acceleration of the mass when it is released from rest.
View Solution