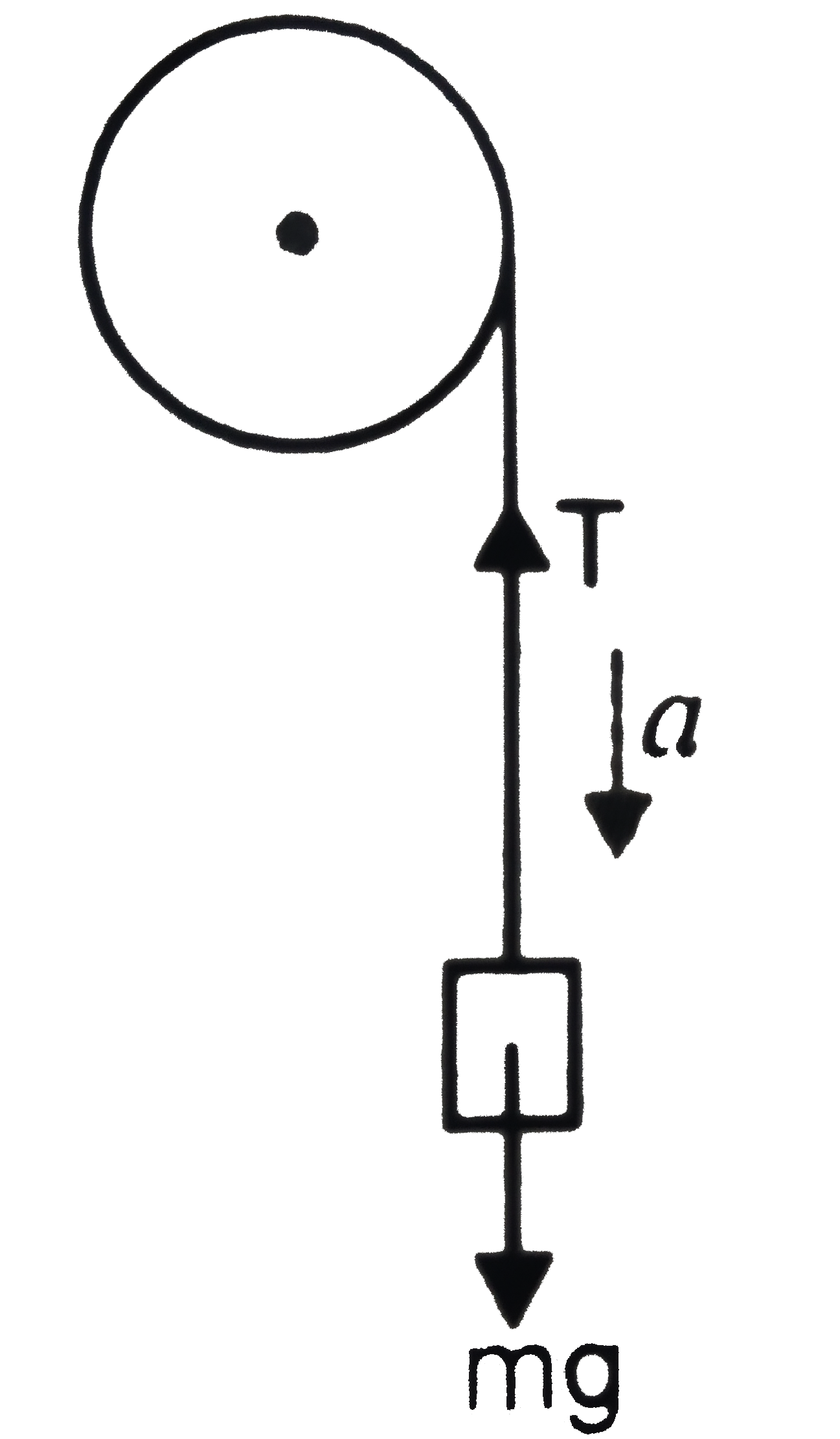
A wheel of radius $6 c m$ is mounted so as to rotate about a horizontal axis through its centre. A string of negligibe mass wrapped round its circumference carries a mass of $0.2 k g$ attrached to its free end. When let fall, the mass descends through $1 m$ in $5 s$ . Calculate the angular acceleration of the wheel, its moment of inertia and tension in the cord.

Video Solution

Text Solution

Verified by Experts

Here, $r = 6 c m = 6 \times 10^{- 2} m$
$m = 0.2 k g, s = 1 m, t = 5 s$ .
If $a$ is acceleration of falling mass, Fig.
from $s = u t + \frac{1}{2} a t^{2}$
$1 = 0 + \frac{1}{2} \times a \times 5^{2}, a = \frac{2}{25} m / s^{2}$
Angular acc. $α = \frac{a}{r} = \frac{2 / 25}{6 \times 10^{- 2}} = 1.33 r a d / s^{2}$
Velocity after $5 s, v = u + a t$
$= 0 + \frac{2}{25} \times 5 = 0.4 m / s$
Angular velocity $ω = \frac{v}{r} = \frac{0.4}{6 \times 10^{- 2}} = \frac{20}{3} r a d / s$
According to the law of conservation of energy
Loss of $P . E =$ Increase in (K.E. of translation $+ K . E .$ of rotation)
$m g h = \frac{1}{2} m v^{2} + \frac{1}{2} I ω^{2}$
$0.2 \times 9.8 \times 1 = \frac{1}{2} \times 0.2 {(0.4)}^{2} + \frac{1}{2} I {(\frac{20}{3})}^{2}$
$0.196 = 0.1 \times 0.16 + I \times \frac{400}{18}$
$0.180 = I \times \frac{400}{18}$
or $I = \frac{0.180 \times 18}{400} = 8.75 \times 10^{- 2} l g m^{2}$
If $I$ is tension in the string, then from $m a = m g - T$
$T = m g - m a = m (g - a)$
$= 0.2 (9.8 - 0.08) = 0.2 \times 9.72$
$T = 1.944 N$

Updated on:21/07/2023

Moment of inertia of a uniform quarter disc of radius $R$ and mass $M$ about an axis through its centre of mass and perpendicular to its plane is $:$
A $\frac{M R^{2}}{2} - M {(\frac{4 R}{3 π})}^{2}$
B $\frac{M R^{2}}{2} - M {(\sqrt{2} \frac{4 R}{3 π})}^{2}$
C $\frac{M R^{2}}{2} + M {(\frac{4 R}{3 π})}^{2}$
D $\frac{M R^{2}}{2} + M {(\sqrt{2} \frac{4 R}{3 π})}^{2}$
A string is wound round the rim of a mounted flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel is
A50 rad $s^{- 2}$
B25 rad $s^{- 2}$
C12.5 rad $s^{- 2}$
D6.25 rad $s^{- 2}$
A fly wheel of $0.4 k g (m^{- 2})$ M.I. and of 0.2 m radius can rotate about its axis. A rope is wrapped around its circumference and pulled with 10 N force. The value of angular acceleration in $r a \frac{d}{{sec}^{2}}$ will be?
A5
B2
C10
D0.8