A uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
To solve the problem, we need to analyze the forces acting on the block and the torque acting on the disc. Here’s a step-by-step solution:
Step 1: Identify the forces acting on the block
When the block of mass m is released, two forces act on it:
- The gravitational force mg acting downward.
- The tension T in the string acting upward.
Step 2: Write the equation of motion for the block
Using Newton's second law, we can write the equation for the block:
mg−T=ma(1)
where a is the acceleration of the block.
Step 3: Analyze the disc and the torque
The tension T also creates a torque on the disc. The torque τ due to the tension is given by:
τ=T⋅R
where R is the radius of the disc.
Step 4: Relate torque to angular acceleration
The torque is also related to the angular acceleration α of the disc:
τ=Iα
For a uniform disc, the moment of inertia I about its center is:
I=12MR2
Thus, we can write:
T⋅R=12MR2α(2)
Step 5: Relate linear acceleration to angular acceleration
Since the string does not slip, the linear acceleration a of the block is related to the angular acceleration α of the disc by:
a=Rα⇒α=aR(3)
Step 6: Substitute α in the torque equation
Substituting equation (3) into equation (2):
T⋅R=12MR2⋅aR
This simplifies to:
T=12Ma(4)
Step 7: Substitute T back into the equation for the block
Now, substitute equation (4) into equation (1):
mg−12Ma=ma
Rearranging gives:
mg=ma+12Ma
mg=a(m+12M)
Step 8: Solve for acceleration a
Now, we can solve for a:
a=mgm+12M
Final Result
Thus, the acceleration of the block is:
a=mgm+12M
---
When the block of mass m is released, two forces act on it:
- The gravitational force mg acting downward.
- The tension T in the string acting upward.
Using Newton's second law, we can write the equation for the block:
mg−T=ma(1)
where a is the acceleration of the block.
The tension T also creates a torque on the disc. The torque τ due to the tension is given by:
τ=T⋅R
where R is the radius of the disc.
The torque is also related to the angular acceleration α of the disc:
τ=Iα
For a uniform disc, the moment of inertia I about its center is:
I=12MR2
Thus, we can write:
T⋅R=12MR2α(2)
Since the string does not slip, the linear acceleration a of the block is related to the angular acceleration α of the disc by:
a=Rα⇒α=aR(3)
Substituting equation (3) into equation (2):
T⋅R=12MR2⋅aR
This simplifies to:
T=12Ma(4)
Now, substitute equation (4) into equation (1):
mg−12Ma=ma
Rearranging gives:
mg=ma+12Ma
mg=a(m+12M)
Now, we can solve for a:
a=mgm+12M
Thus, the acceleration of the block is:
a=mgm+12M
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
10 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
14 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
A disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View Solution
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgThe M.I. of a uniform disc about a diameter is I. Its M.I. about an axis perpendiçular to its plane and passing through a point on its rim is
A51B61CID4IThe M.L. of a uniform disc about the diameter is 1. Its M.I. about an axis perpendicular to its plane and passing through a point on its rim is
A4IB5IC6IDI
A uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionA uniformaly thick wheel with moment of inertia I and radius R is free to rotate about its centre of mass (see fig). A massless string is wrapped over its rim and two blocks of masses m1andm2(m1>m2) are attached to the ends of the strung. The system is released from rest. The angular speed of the wheel when m1 descents by a distance h is :
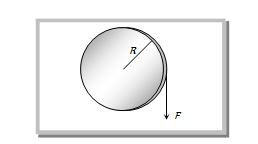
View SolutionA uniform disc of radius R and mass M can rotate on a smooth axis passing through its centre and perpendicular to its plane. A force F is applied on its rim. See fig. What is the tangential acceleration
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View Solution
