Question

A body A moving with momentum P collides one-dimensionally with another stationary body B of same mass. During impact, A gives impulse J to B. Then which of the following is/are correct ?
(a) The total momentum of A and B is P before and after impact and (P - J) during the impact.
(b) During the impact, B gives impulse of magnitude J to A.
(c ) The coefficient of restitution is $[\frac{2J}{P}-1]$
(d) The coefficient of restitution is $[\frac{2J}{P}+1]$

Options

A. Only (a) is correct
B. (a) and (c ) are correct
C. (b) and (c ) are correct
D. Only (c ) is correct

Answer

C

Explanation

According to the question, a collision between two bodies (A and B) is shown in the figure below,

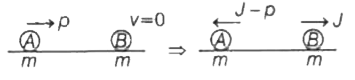
So, the coefficient of restitution
`e = ("Relative velocity of separation")/("Relative velocity of approach")`
`rArr e = ((J-p)/(m) + (J)/(m))/((p)/(m) - 0) = (2J)/(P) - 1 " "(because v = (m v)/(m) = (p)/(m))`
During the impact, B gives impulse
`J_(B) = p + J - p = J`
Hence, the statement (b) and (c ) are correct.