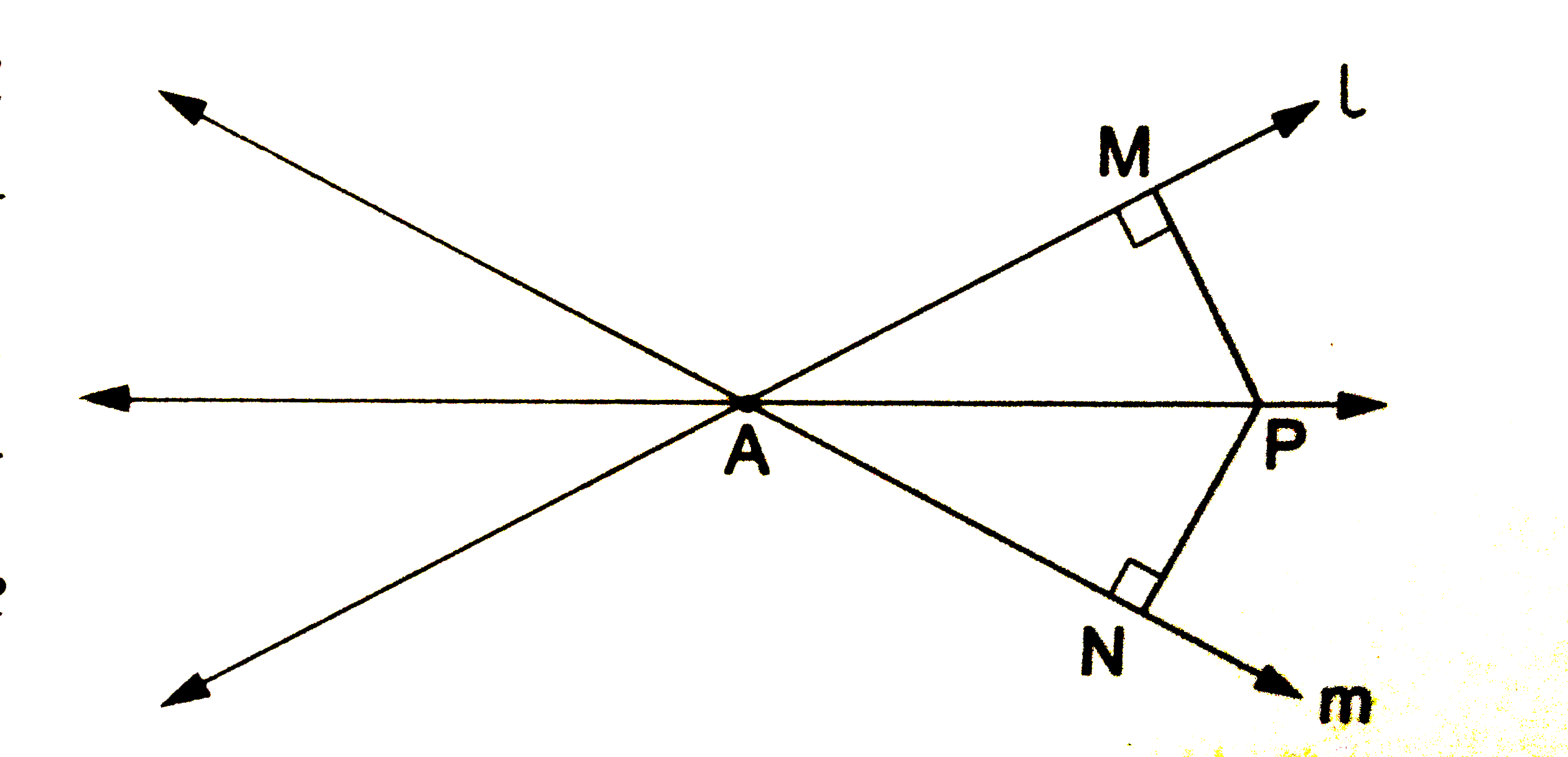
P is a point equidistant from two lines l and m intersecting at point A(see Fig. 7.38). Show that the line AP bisects the angle between them.
Perpendicular from P to l and m
PB=PC
∠PBA=∠PCA
In∠ABPand∠ACP
∠ABP=∠ACP
AP=AP
BP=CP
∠ABP≅∠ACP
=AP is angle bisector of ∠BAC
Topper's Solved these Questions
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.1
8 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.8
10 Videos
Similar Questions
P is a point equidistant from two lines l and m intersecting at point A(see Fig. 7.38). Show that the line AP bisects the angle between them.
View SolutionIn figure P is a point equidistant from the lines l and m intersecting at point A. Show that the line n (along AP) bisects the angle between l and m.

View Solution
Knowledge Check
The loucs of a point which is a equidistant from two non-intersecting lines l and m is a _____
Astraight line parallel to the line lBStraight line parallel to the line mCStraight line parallel to the line l and m and midway between themDstraight line that intersects both the line l and m
P is a point equidistant from two lines l and m intersecting at a point A see in figure, Show that AP bisects the angle between them. Figure
View SolutionP is a point equidistant from two lines l and m intersecting at a point A, as shown in the given figure. Show that the line AP bisects tha angle between them.
View SolutionThe locus of a point equidistant from two intersecting lines is
View SolutionTwo line segments may intersect at two points
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
View Solution
