P is a point equidistant from two lines l and m intersecting at a point A, as shown in the given figure. Show that the line AP bisects tha angle between them.
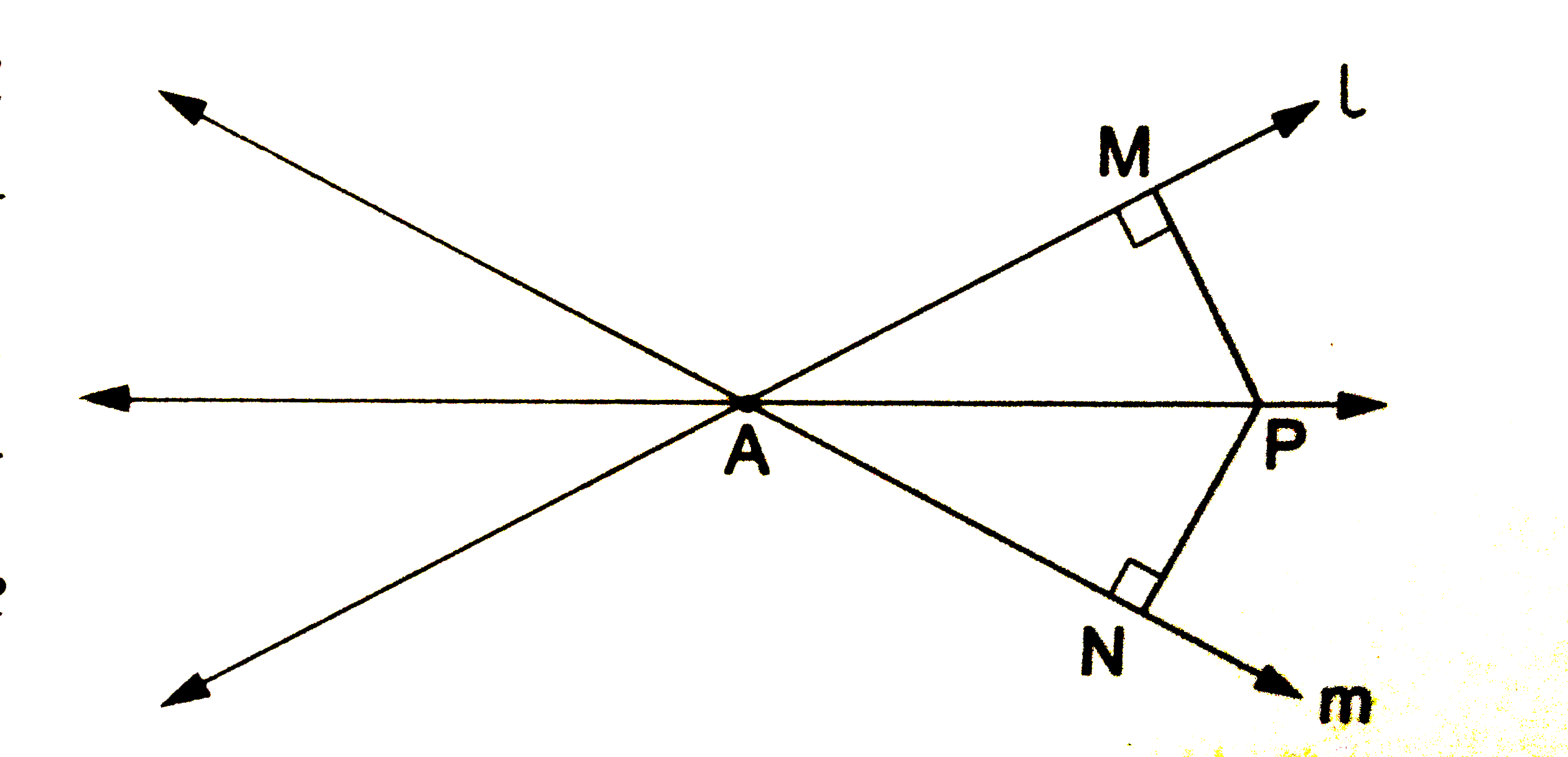
GIVEN Two lines l and m intersecting at a point A and P is a point such that PM = PN, where PM⊥landPN⊥m.
TO PROVE ∠PAM=∠PAN.
PROOF In ΔPAMandΔPAN, we have
∠PMA=∠PNA=90∘
PM=PN (given)
AP=AP (common)
∴ ΔPAM≅ΔPAN (by RHS-criteria).
∴ ∠PAM=∠PAN (c.p.c.t.).
Hence, the line PA bisects the angle between l and m.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
P is a point equidistant from two lines l and m intersecting at point A(see Fig. 7.38). Show that the line AP bisects the angle between them.
View SolutionP is a point equidistant from two lines l and m intersecting at a point A see in figure, Show that AP bisects the angle between them. Figure
View Solution
Knowledge Check
The loucs of a point which is a equidistant from two non-intersecting lines l and m is a _____
Astraight line parallel to the line lBStraight line parallel to the line mCStraight line parallel to the line l and m and midway between themDstraight line that intersects both the line l and m
In figure P is a point equidistant from the lines l and m intersecting at point A. Show that the line n (along AP) bisects the angle between l and m.

View SolutionThe locus of a point equidistant from two intersecting lines is
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
View SolutionTwo lines "AB" and "CD" intersect at a point O such that ∠BOC+∠AOD=280∘, as shown in the figure. Find all four angles.
View SolutionTwo lines AB and CD intersect at a point O such that ∠BOC+∠AOD=280∘, as shown in the figure. Find all the four angles.
View SolutionP is a point on either of the two lines y−√3|x|=2 at a distance 5 units from their point of intersection The coordinates of the foot of the perpendicular from P on the bisector of the angle between them are
View Solution