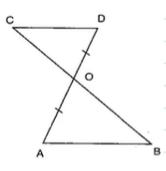
Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see Fig. 7.15). Show that
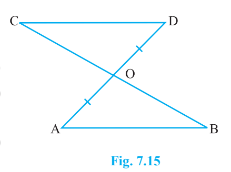
(i) ΔAOB≅ΔDOC
(ii) O is also the mid-point of BC
Given:
AB is parallel to another line segment CD.
O is the midpoint of AD
In △AOBand△DOC
∠AOB=∠COD
(Vertically opposite angle )
∠BAO=∠CDO ...(Given AB parallel to DC and AD meet both lines so alternate angles are equal)
AO=OD ....(O is the midpoint of AD )
△AOB≅△DOC...(ASAtest)
So, BO=COThen, O is the midpoint of BC.
Similar Questions
Line segment AB is parallel to another line segment CD. O is the midpoint of AD (see the given figure). Show that
(i) △AOB=△DOC
(ii) O is also the midpoint of BC
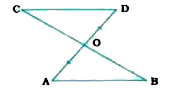
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC
View Solution
Knowledge Check
O is mid-point of AB. The magnetic field at O is
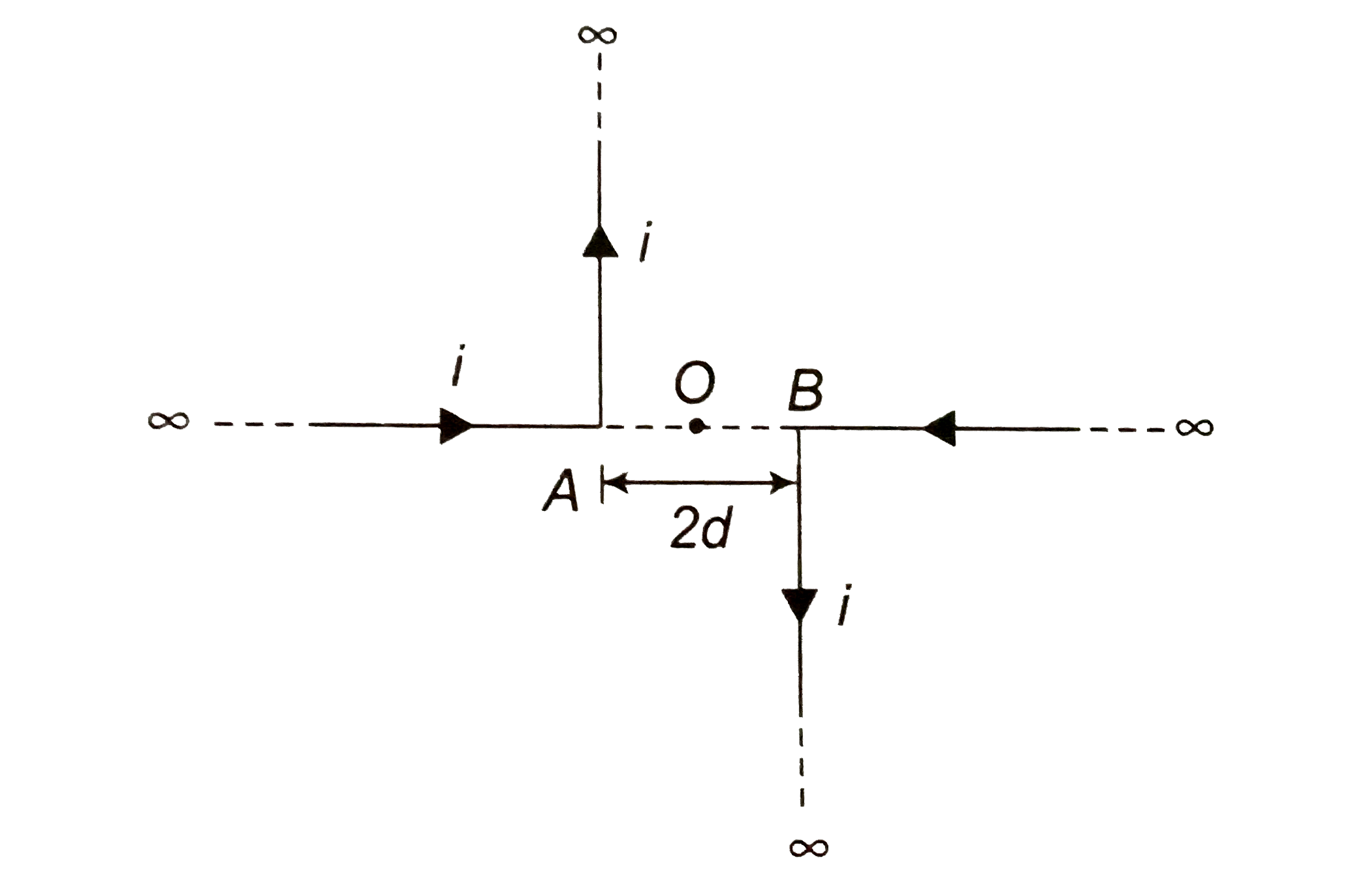 Aμ0i2πd,⊗Bμ0iπd,⊙C2μ0iπd,⊗D4μ0iπd,⊗
Aμ0i2πd,⊗Bμ0iπd,⊙C2μ0iπd,⊗D4μ0iπd,⊗
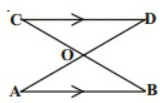
In Figure, line segment AB is parallel to another line segment CD . O is the mid-point of AD . Show that: (i)AOB≅DOC (ii)O is also the mid-point of BC.
View SolutionIn the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.

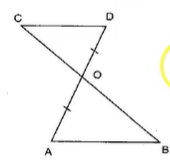
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: O is also the mid-point of BD
View SolutionIn Figure, if line segment AB is parallel to the line segment CD, what is the value of y? (a)12 (b) 15 (c) 18 (d) 20
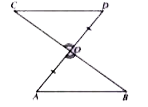
View SolutionIn the figure AB || CD, AD and BC intersect at o and O is mid-point of AD. Show that
(i) ΔAOB≅ΔDOCand(ii)OB=OC.
View SolutionAD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

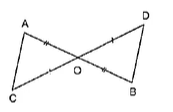
View SolutionIn Figure O is the mid-point of AB and CD. Prove that AOC≅ BOD (b) AC=BD (iii) AC∣∣BD
View Solution
