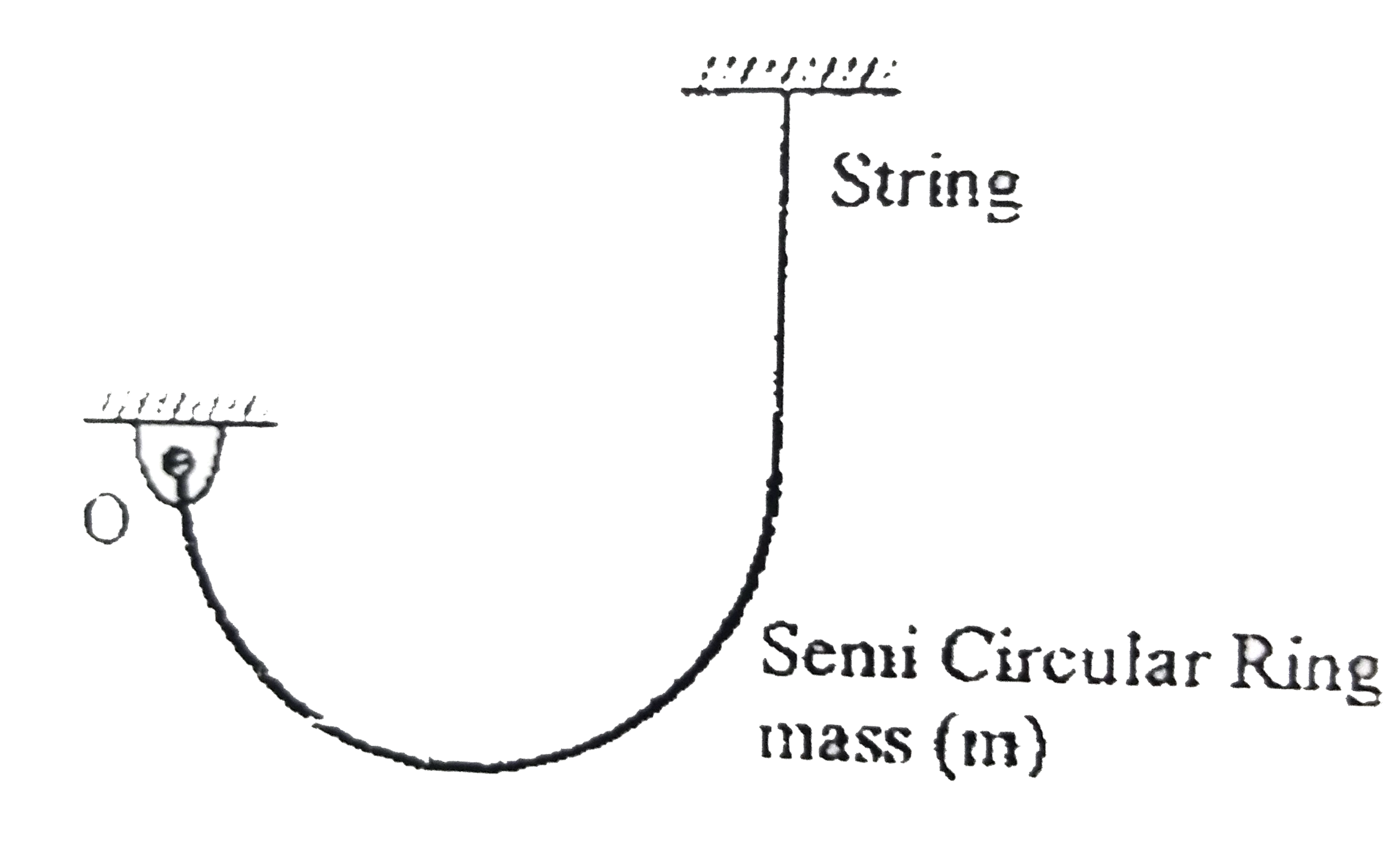
A uniform semi circular ring of radius R and mass m is free to oscillate about its one end in its vertical plane as shown in the figure. Find time period of SHM of its centre of mass of the ring (take )
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View Solution
Knowledge Check
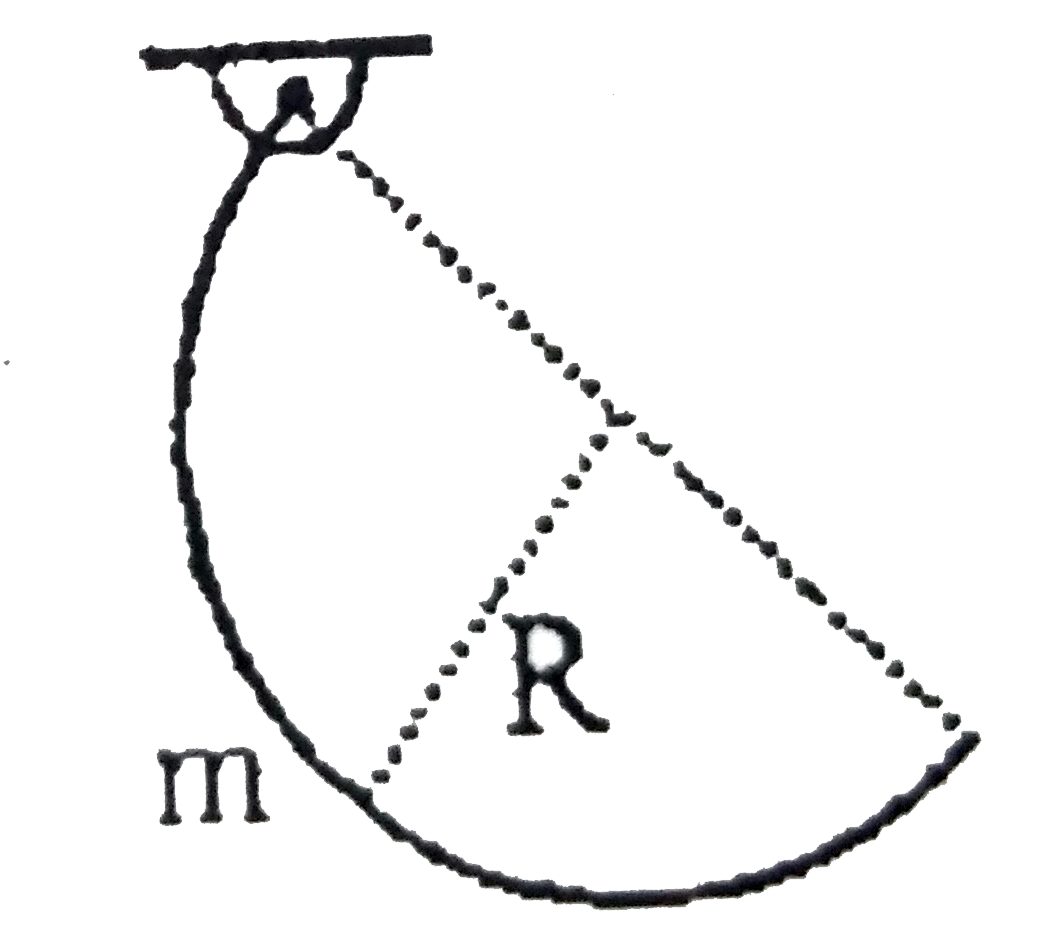
The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
 ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.A uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√2RgBπ√2RgCπ2√RgDπ√R2gFor a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
A rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

View SolutionA half ring of mass m, radius R is hanged at its one end its one end in verical plane and if free to socilalte in its plane.
Find oscillations frequency of the half ring.
_E01_109_Q01.png)
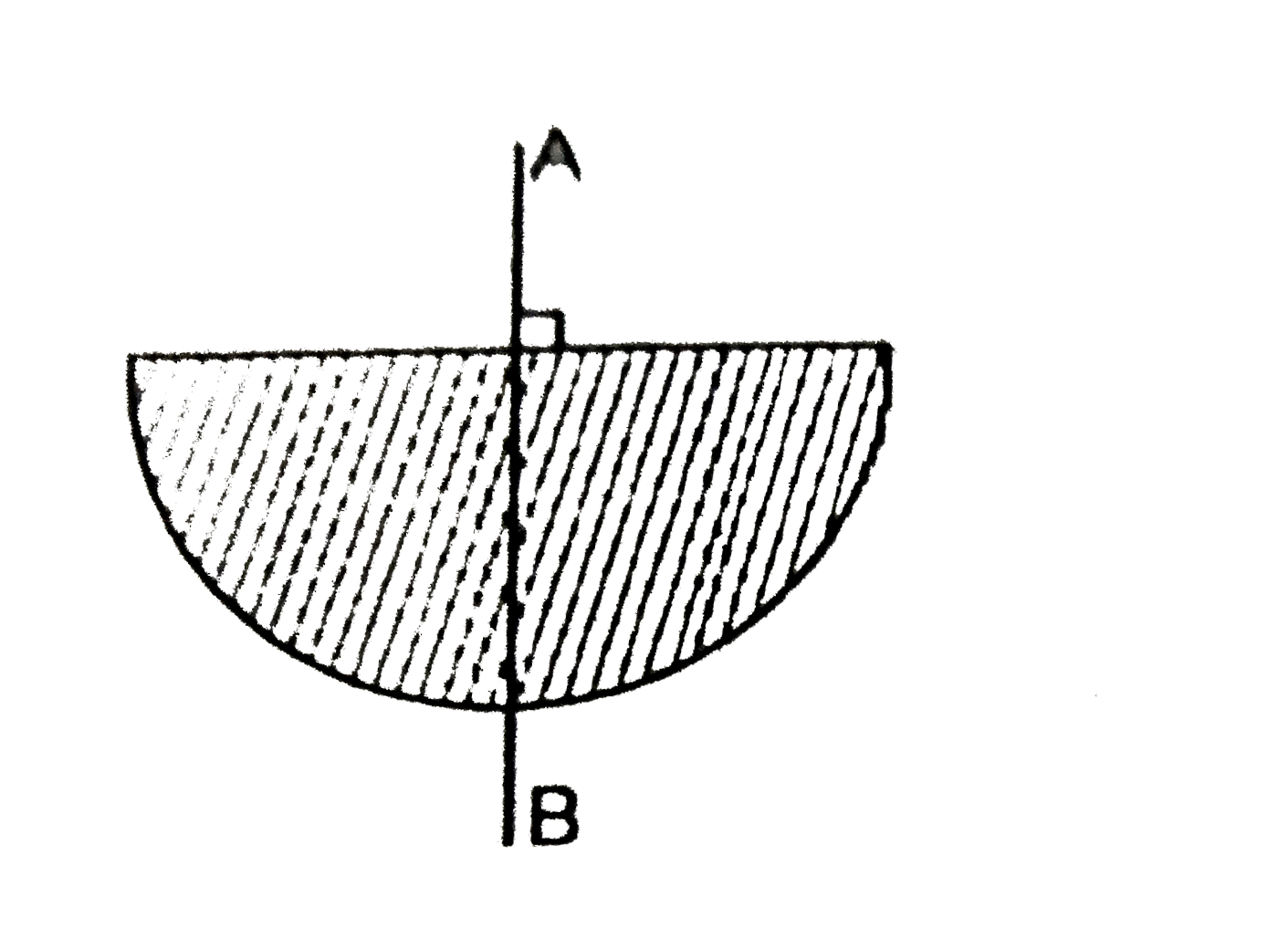
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
View SolutionA particle of mass m is placed on centre of curvature of a fixed, uniform semi-circular ring of radius R and mass M as shown in figure. Calculate:
(a) interaction force between the ring and the particle and
(b) work required to displace the particle from centre of curvature to infinity.

View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View Solution

