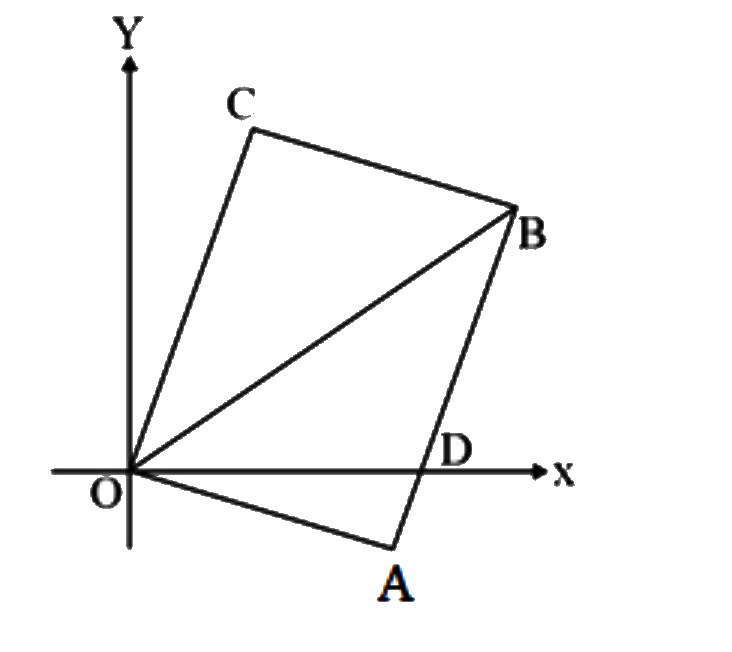
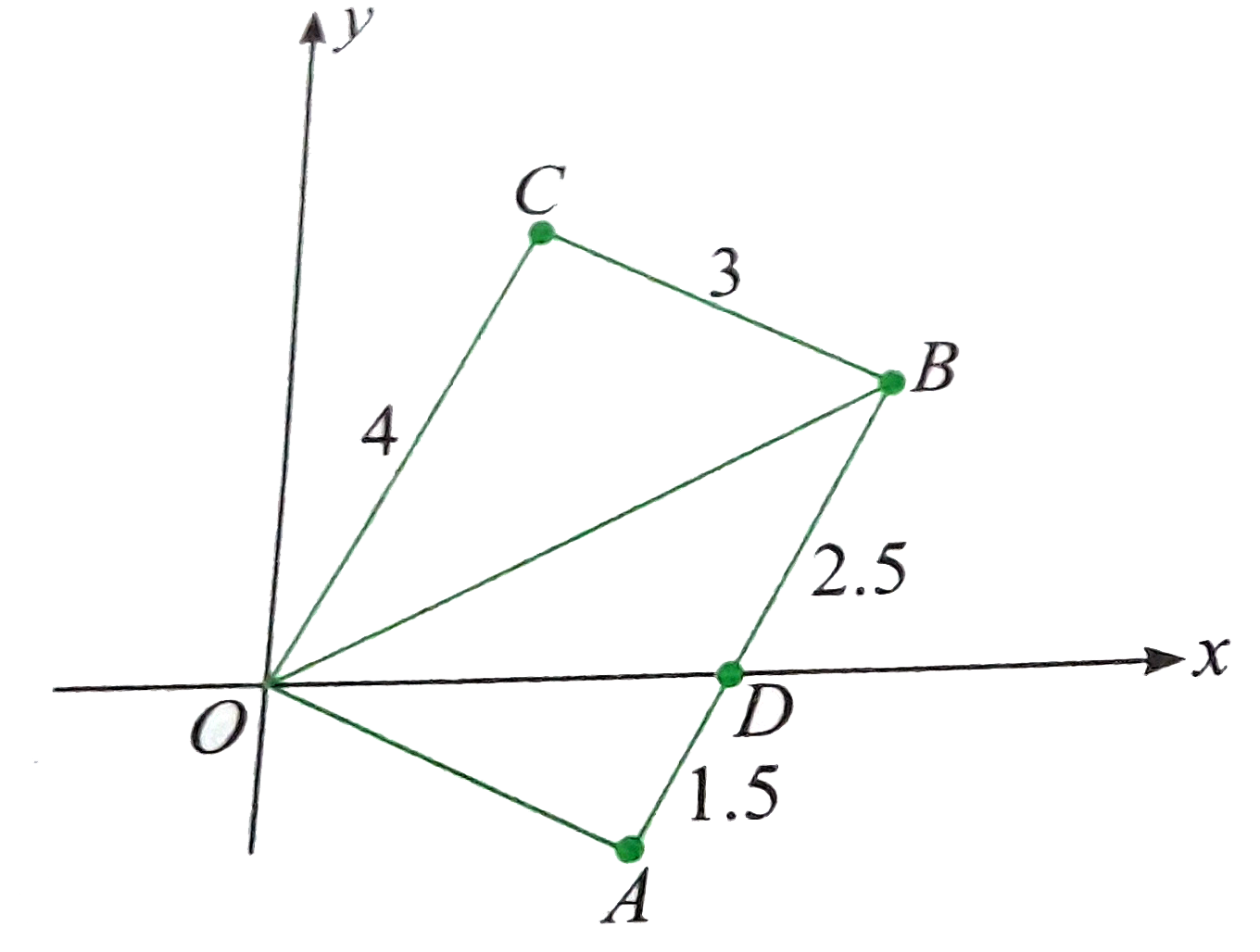
In the given figure, OABC is a rectangle. Slope of OB is
1/4
1/3
1/2
Cannot be determined
The correct Answer is:C
Clearly, OB=5
So, OAOB=35=1.52.5=ADDB
Thus, OD bisects ∠AOB.
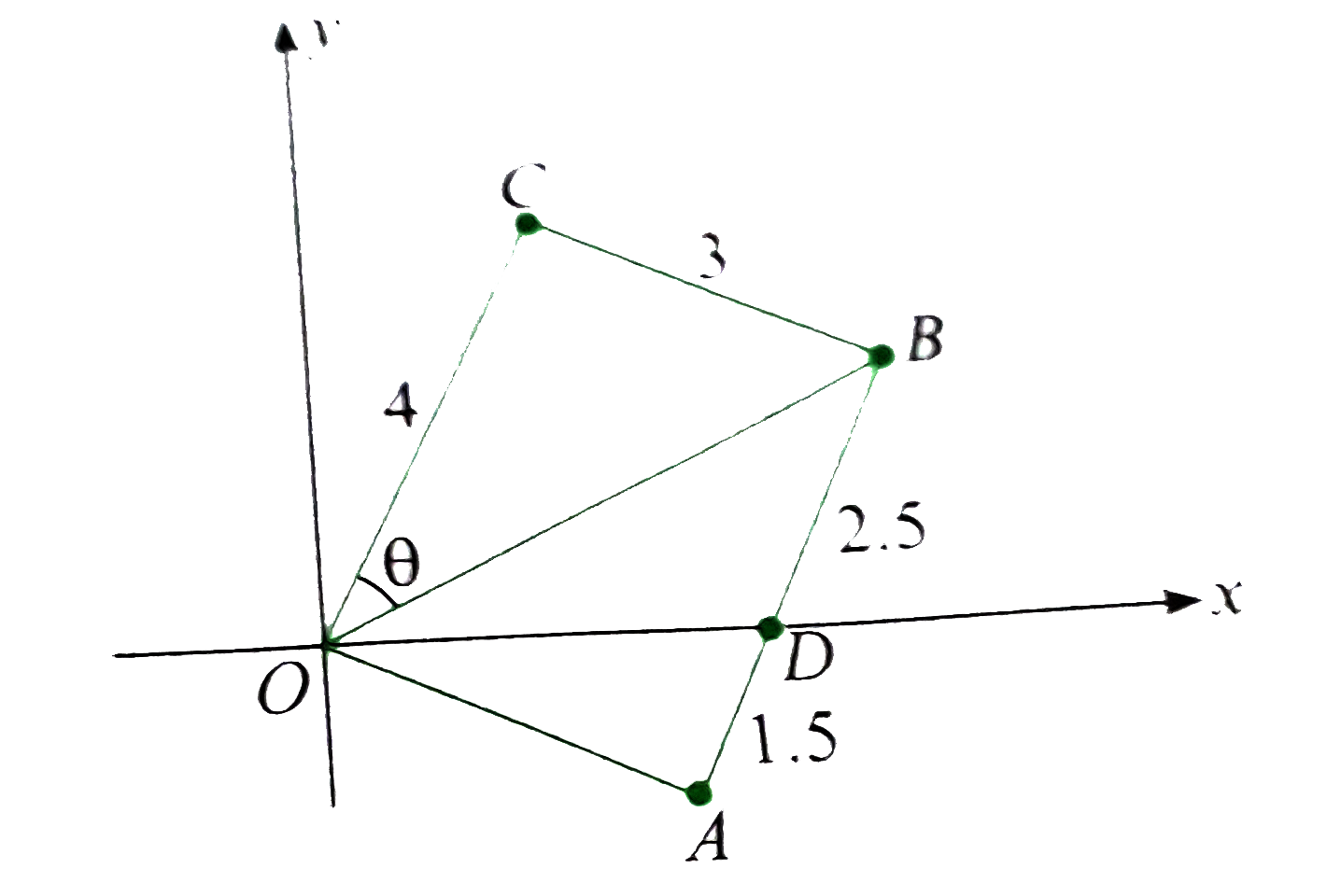
Let ∠BOC=θ. Then tanθ=34
∴∠BOC=12∠AOB=12(90∘−θ)
∴ Slope of OB=tan(1)2(90∘−θ)=tan45∘−tan.θ21+tan45∘+tan.θ2
Now, tanθ=34
⇒2tan.θ21−tan2.θ2=34
3−3tan2.θ2=8tan.θ2
⇒3tan2.θ2+8tan.θ2−3=0
⇒(3tan.θ2−1)(tan.θ2+3)=0
So, tan.θ2=13 (∵θ2is acute)
∴ Slope of OB=1−131+13=12
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Knowledge Check
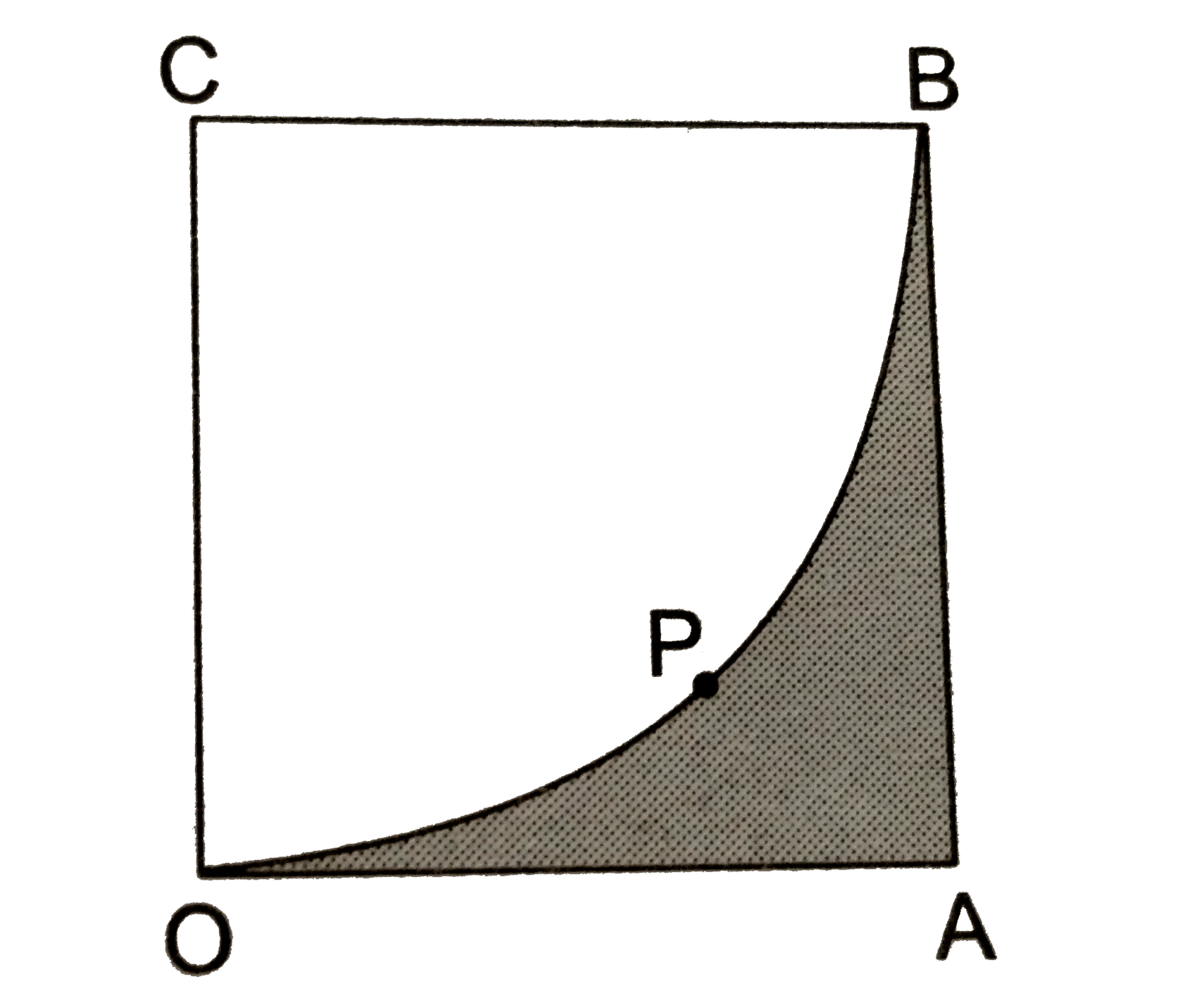
In the given figure, ABCD is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If AD=√25 cm then area of the rectangle is
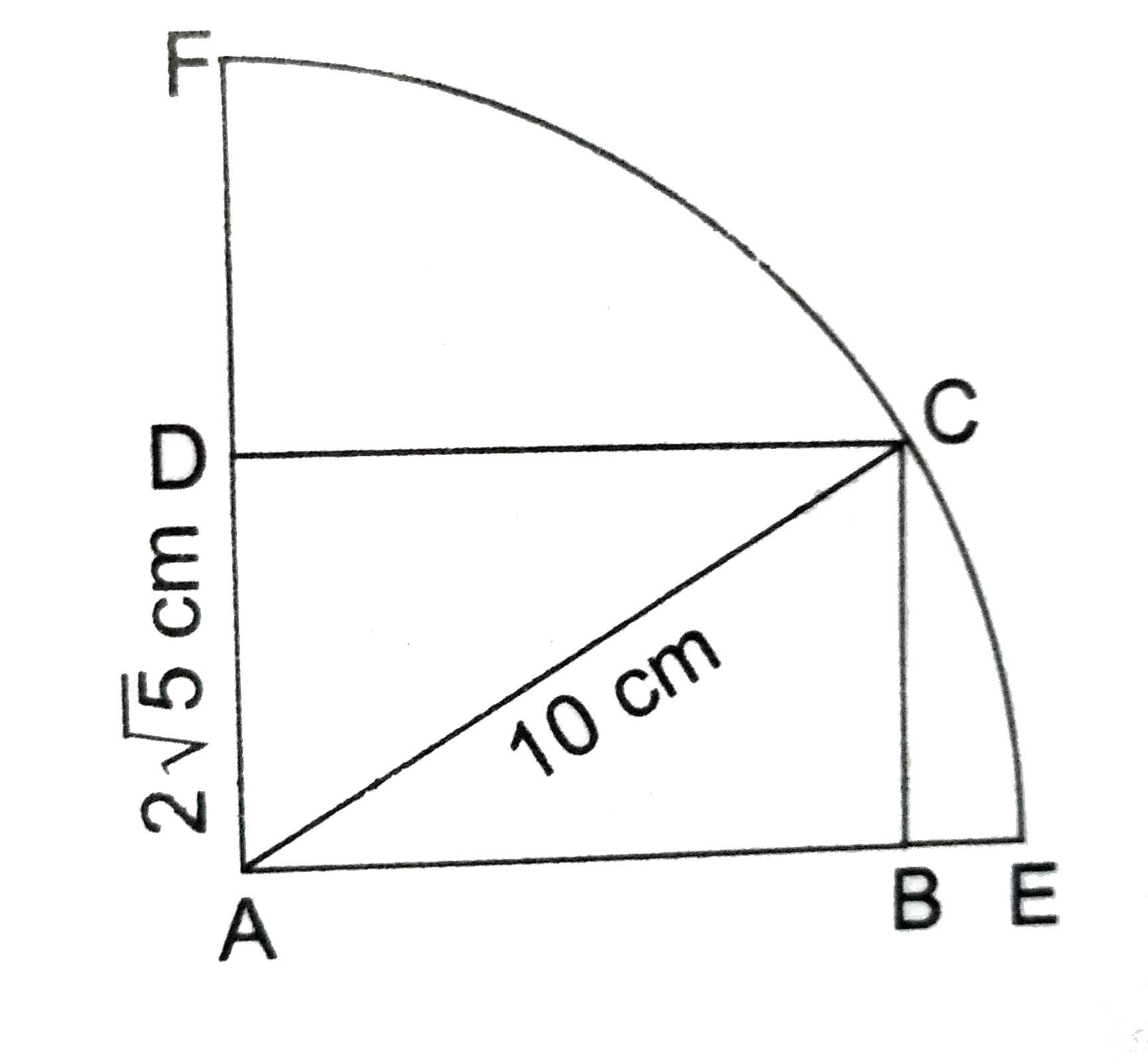 A32cm2B40cm2C44cm2D48cm2
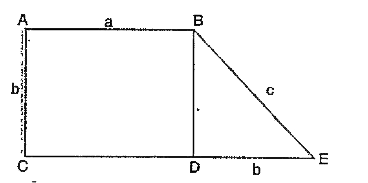
A32cm2B40cm2C44cm2D48cm2What is the area of the given figure ? ABCD is a rectangle and BDE is an isosceles right triangle.
 AabBab2CcabDb(a+b/2)
AabBab2CcabDb(a+b/2)In the given figure, a ||gm ABCD and a rectangle ABEF are of equal area. Then,
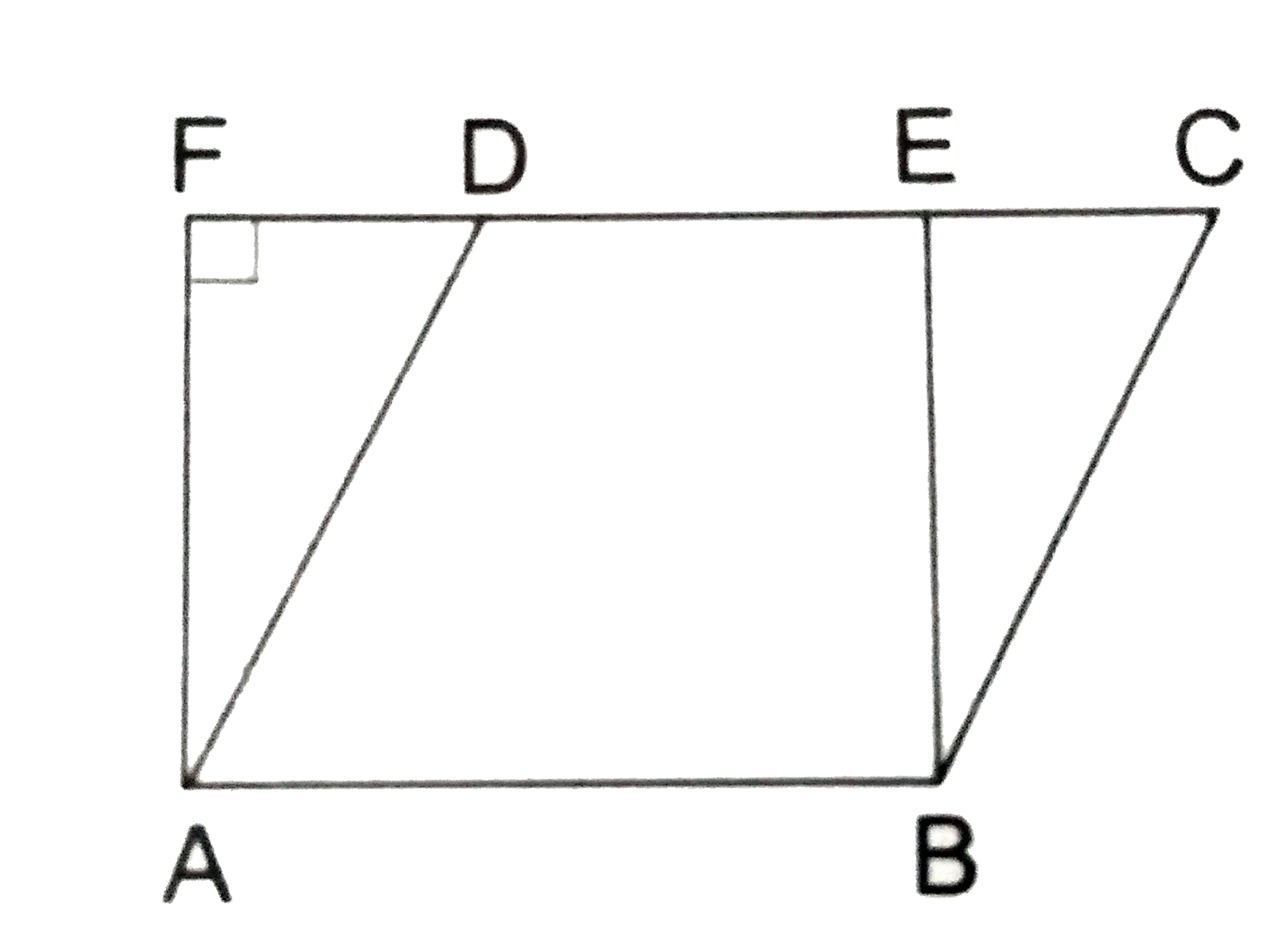 Aperimeter of ABCD = perimeter of ABEFBperimeter of ABCD < perimeter of ABEFCperimeter of ABCD > perimeter of ABEFDperimeter of ABCD =12 perimeter of ABEF
Aperimeter of ABCD = perimeter of ABEFBperimeter of ABCD < perimeter of ABEFCperimeter of ABCD > perimeter of ABEFDperimeter of ABCD =12 perimeter of ABEF
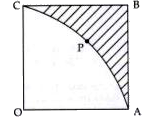
In the given figure, OABC is a square of side 7cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
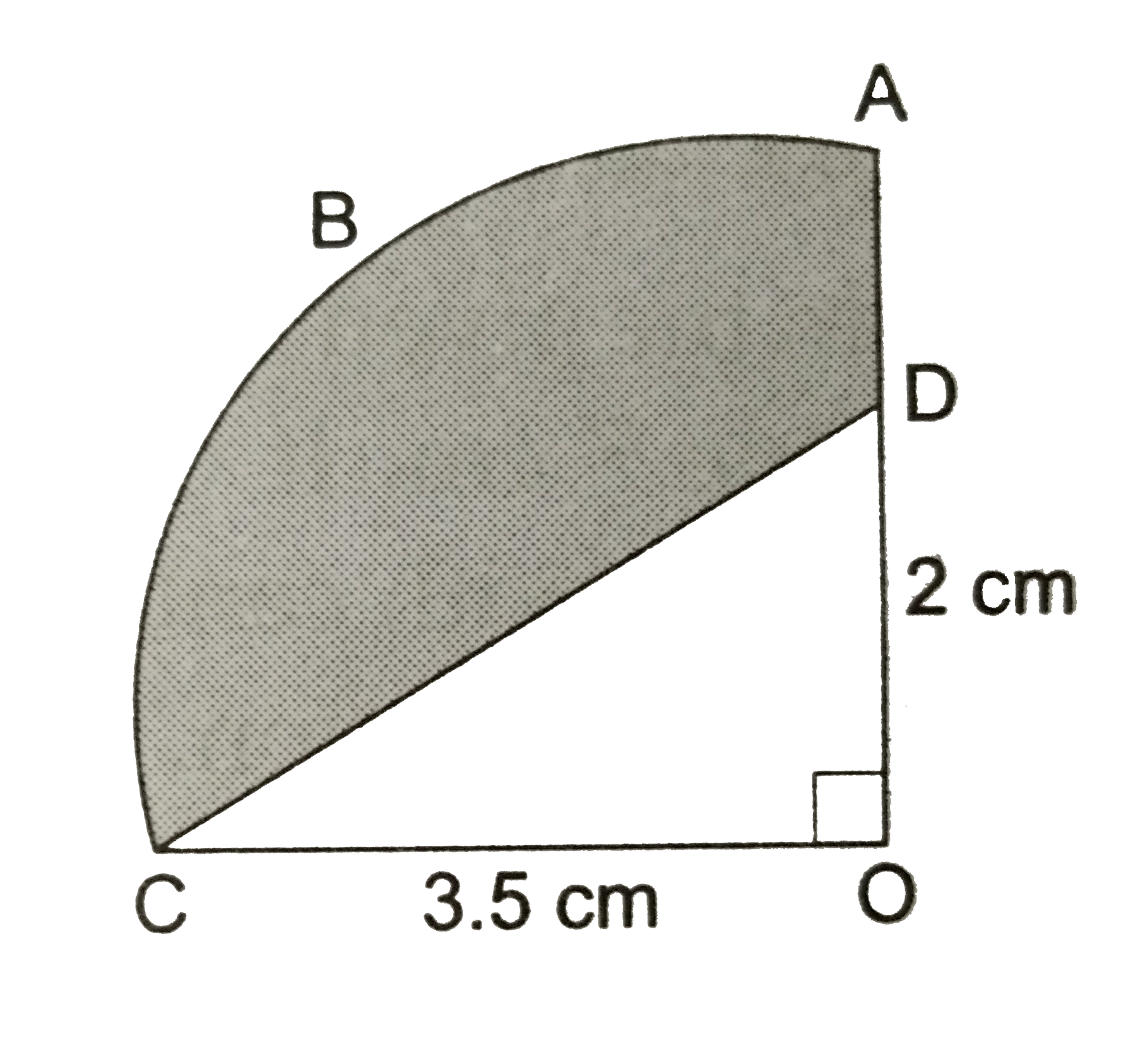
View SolutionIn the given figure OABC is a quadrant of a circle with centre O and radius 3.5cm.If OD=2cm,find the area of the shaded region.
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
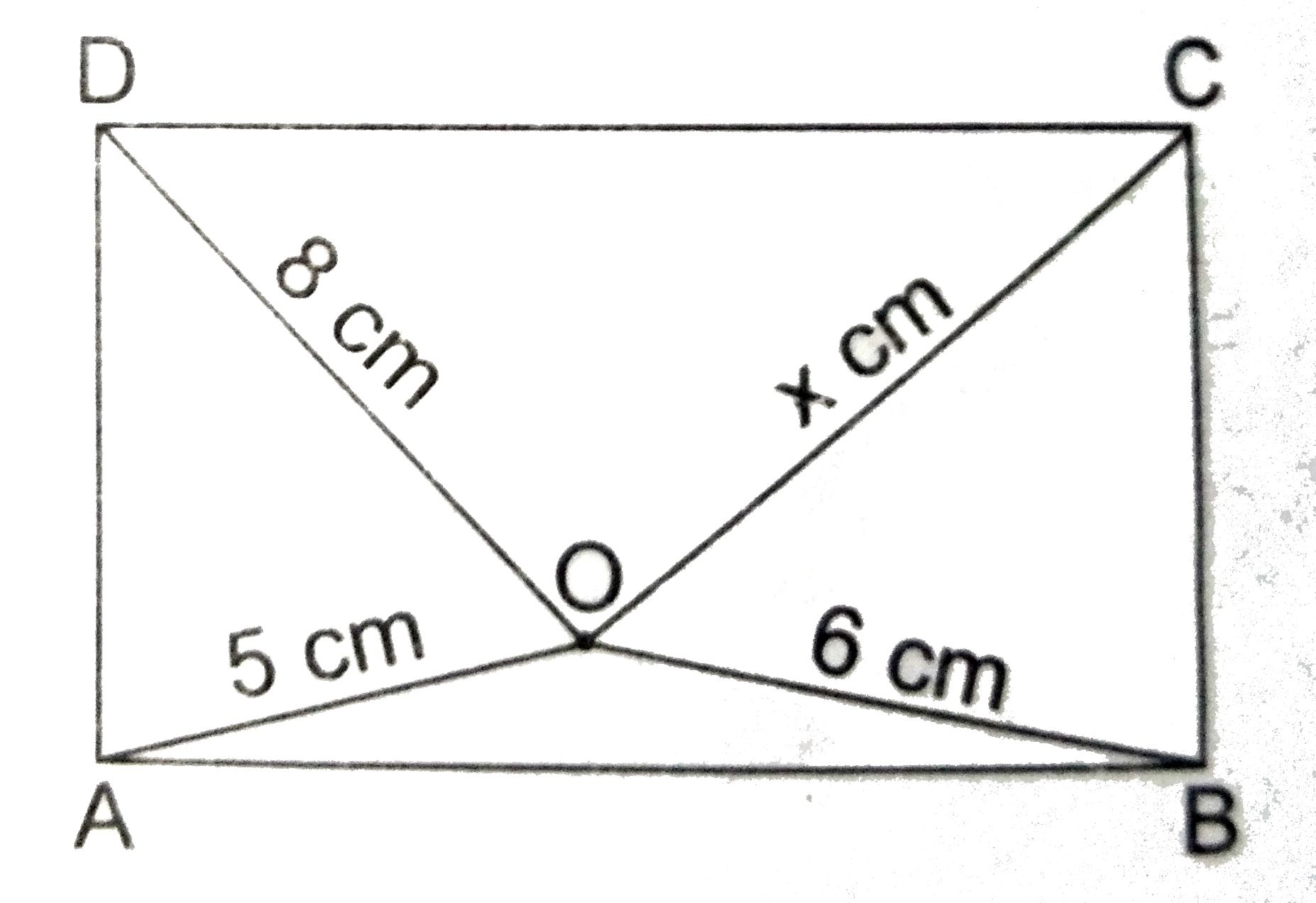
View SolutionIn the given figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region.
View SolutionIn the given figure, if PQRS is a rectangle, then what type of a triangle is PTQ?

View Solution