From a point, P perpendicular PM and PN are drawn to x and y axes, respectively. If MN passes through fixed point (a,b), then locus of P is
xy=ax+by
xy=ab
xy=bx+ay
x+y=xy
The correct Answer is:C
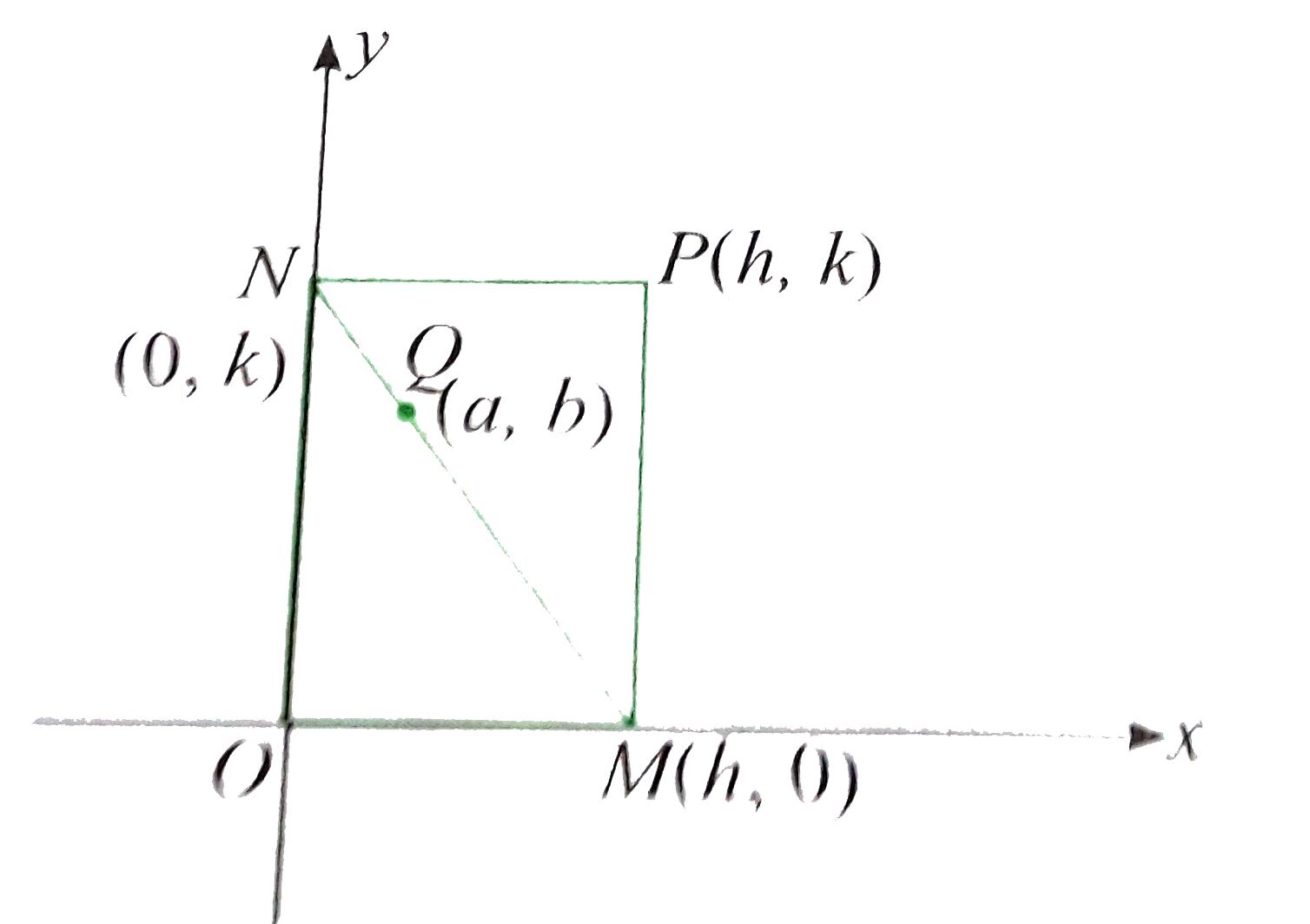
Let P(h,k)
So, points M and N are (h,0) and (0,k), respectively. MN passes through the point Q(a,b)
So, M,N and Q are collinear.
∴ Slope of MN=Slope of QM
∴kh=b−0a−h
∴ak−hk=−bh
So locus is bx+ay=xy.
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Multiple)
Explore 13 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Comprehension)
Explore 10 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.6
Explore 9 Videos
- COORDINATE SYSTEMBook:CENGAGEChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGEChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
Knowledge Check
A circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point (x1,y1), the locus of the centre of the circle, is
Ax1x+y1y=1Bx1y=x1y1Cxy1+yx1=2Dx1x+y1y=2
Let A,B,C be the feet of perpendicular drawn from a point P to x,y and z-axes respectively. Find the coordinates of A,B,C if coordinates of P are : (3,4,2)
View SolutionLet A,B,C be the feet of perpendicular drawn from a point P to x,y and z-axes respectively. Find the coordinates of A,B,C if coordinates of P are : (4,−2,−6)
View SolutionLet A,B,C be the feet of perpendicular drawn from a point P to x,y and z-axes respectively. Find the coordinates of A,B,C if coordinates of P are : (4,−3,−7)
View SolutionLet A,B,C be the feet of perpendicular drawn from a point P to x,y and z-axes respectively. Find the coordinates of A,B,C if coordinates of P are : (3,−5,1)
View SolutionFrom a variable point on the tangent at the vertex of a parabola y2=4ax, a perpendicular is drawn to its chord of contact. Show that these variable perpendicular lines pass through a fixed point on the axis of the parabola.
View SolutionLet P be a variable point. From P tangents PQ and PR are drawn to the circle x2+y2=b2 if QR always touch the parabola y2=4ax then locus ofP is
View SolutionThe locus of the foot of the perpendicular drawn from origin to a variable line passing through fixed point (2,3) is a circle whose diameter is
View Solution

