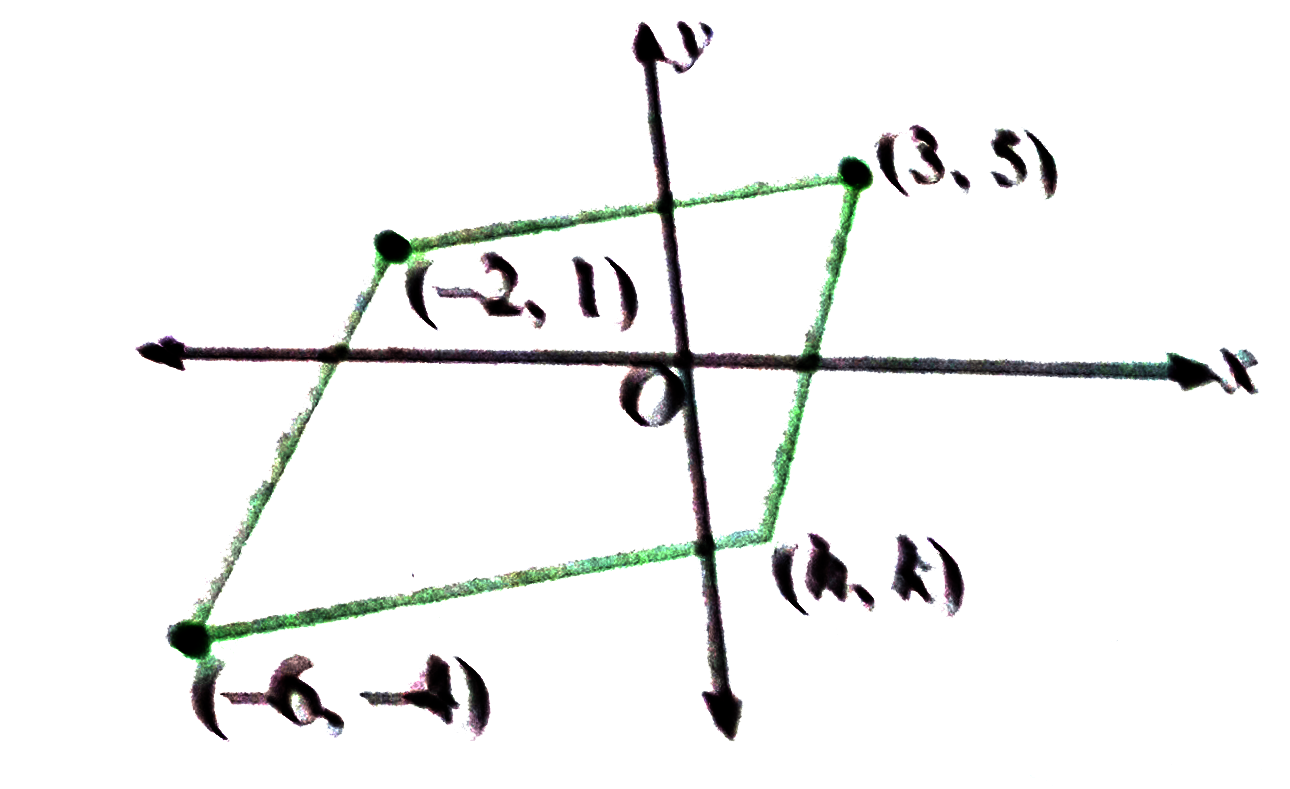
If (−6,−4),(3,5),(−2,1) are the vetices of a prallelogram. Then the remaining vertex can be

A

(0,−1)

B

(7,10)

C

(-1,0)

D

(−11,−8)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B, C, D

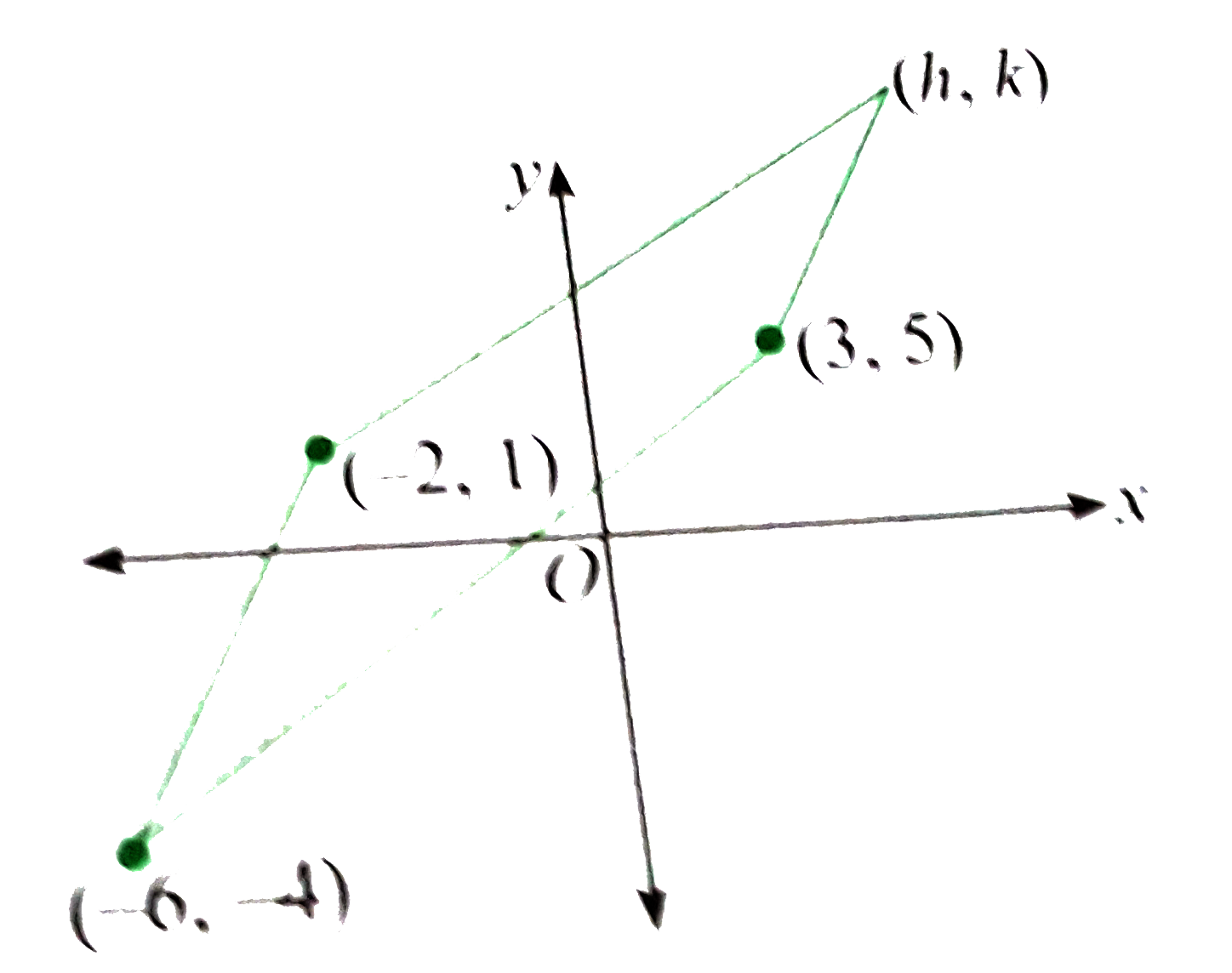
If the remaining vertex is (k,k) then
ocr_image
h−2=−6+3,k+1=5−4
or h=−1,k=0
ocr_image
h+3=−6,k+5=−4+1
or h=−11,k=−8
ocr_image
h−6=3−2,k−4=5+1
or h=7,k=10

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If (-6, -4), (3, 5), (-2, 1) are the vertices of a parallelogram, then remaining vertex can be

    A(0, -1)
    B(-1, 0)
    C(-11, -8)
    D(7, 10 )

  • If (−6,−4) and (3,5) are the extremities of the diagonal of a parallelogram and (−2,1) is its third vertex , then its fourth vertex is

    A(-1,0)
    B(0,-1)
    C(-1,1)
    Dnone of these

  • Points (4, -1), (6, 0), (7, 2) and (5, 1) are joined to be a vertex of a quadrilateral. What will be the structure?

    ARhombus
    BParallelogram
    CSquare
    DRectangle