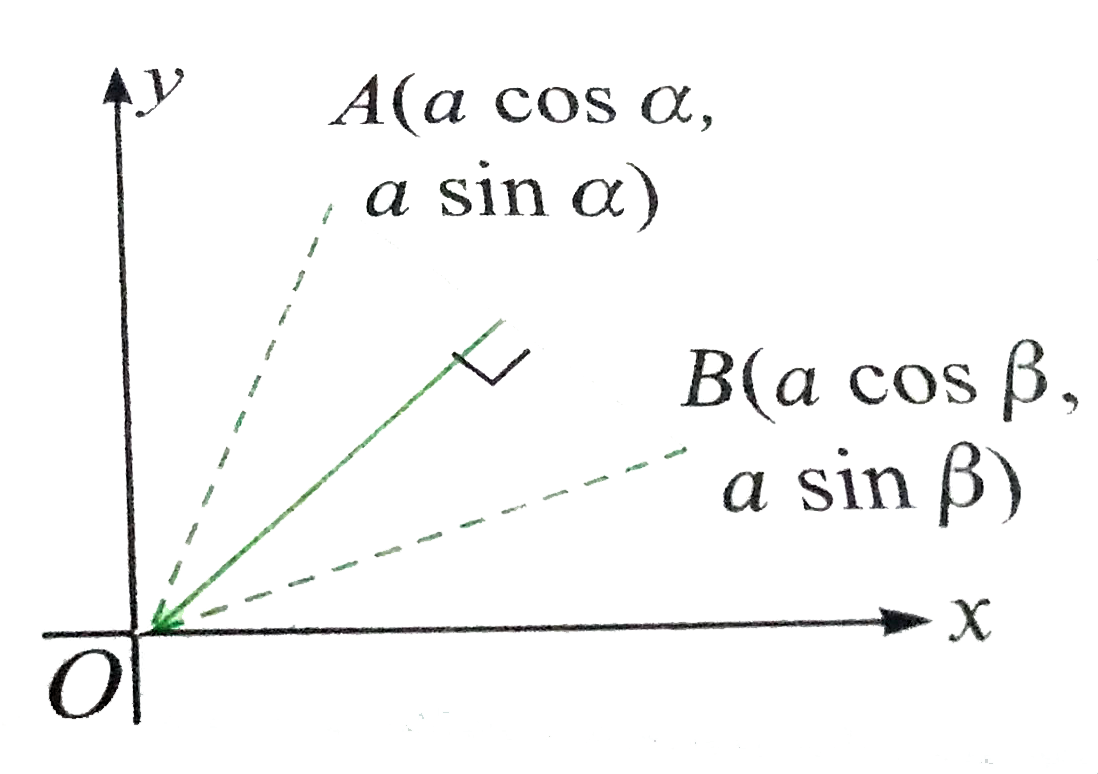
If a straight line through the origin bisects the line passing through

Equation of straight line passing through origin
AY=mx,
BY=C
CX= my
DX=C
Which of the following straight lines passes through the origin?
Ax + y = 4
B $x^{2} + y^{2} = - 6$
Cx + y =5
Dx =4y
The lines parallel to the axes and passing through the point (4, -5) are
A $x = - 5, y = 4$
B $x = 5, y = - 4$
C $x = 4, y = - 5$
D $x = - 4, y = 5$

If a straight line through the origin bisects the line passing through the given points $(a cos α, a sin α)$ and $(a cos β, a sin β),$ then the lines are perpendicular are parallel have an angle between them of $\frac{π}{4}$ none of these