Find potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
Ring can be considered to be made of large number of point masses (m1,m2…..etc)
VP=−Gm1√R2+x2−Gm2√R2+x2−...
=−G√R2+x2(m1+m2...)=−GM√R2+x2,whereM=m1+m2+m3+....
Potential at centre of ring =−G.MR
 .
.
Topper's Solved these Questions
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:SOLVED MISCELLANEOUS PROBLEMS
Explore 5 Videos
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:EXAMPLE
Explore 2 Videos
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Advance level Problems
Explore 35 Videos
- NUCLEAR PHYSICSBook:RESONANCEChapter:NUCLEAR PHYSICSExercise:Advanced level solutions
Explore 16 Videos
Similar Questions
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
Compound pendulum are made of :
(a) A rod of length l suspended through a point located at distance l/4 from centre of rod.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform square plate of edge a suspended through a corner.
(d) A uniform disc of mass m and radius r suspeneded through a point r/2 away from the centre.
Find the time period in each case.
View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionWhat is the gravitational potential energy of a particle of mass m kept at a distance x from the centre of a disc of mass M on its axis ? The radius of the disc is R.
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the kinetic energy needed to project a body of mass m from the centre of a ring of mass M and radius R so that it will never comne back.
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
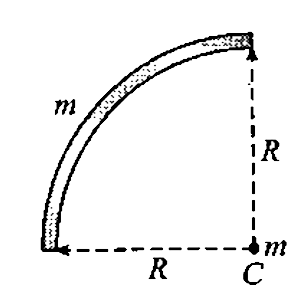
View Solution