Calculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
Consider a elemental ring of radius r and thickness dr on surface of disc as shown in figure
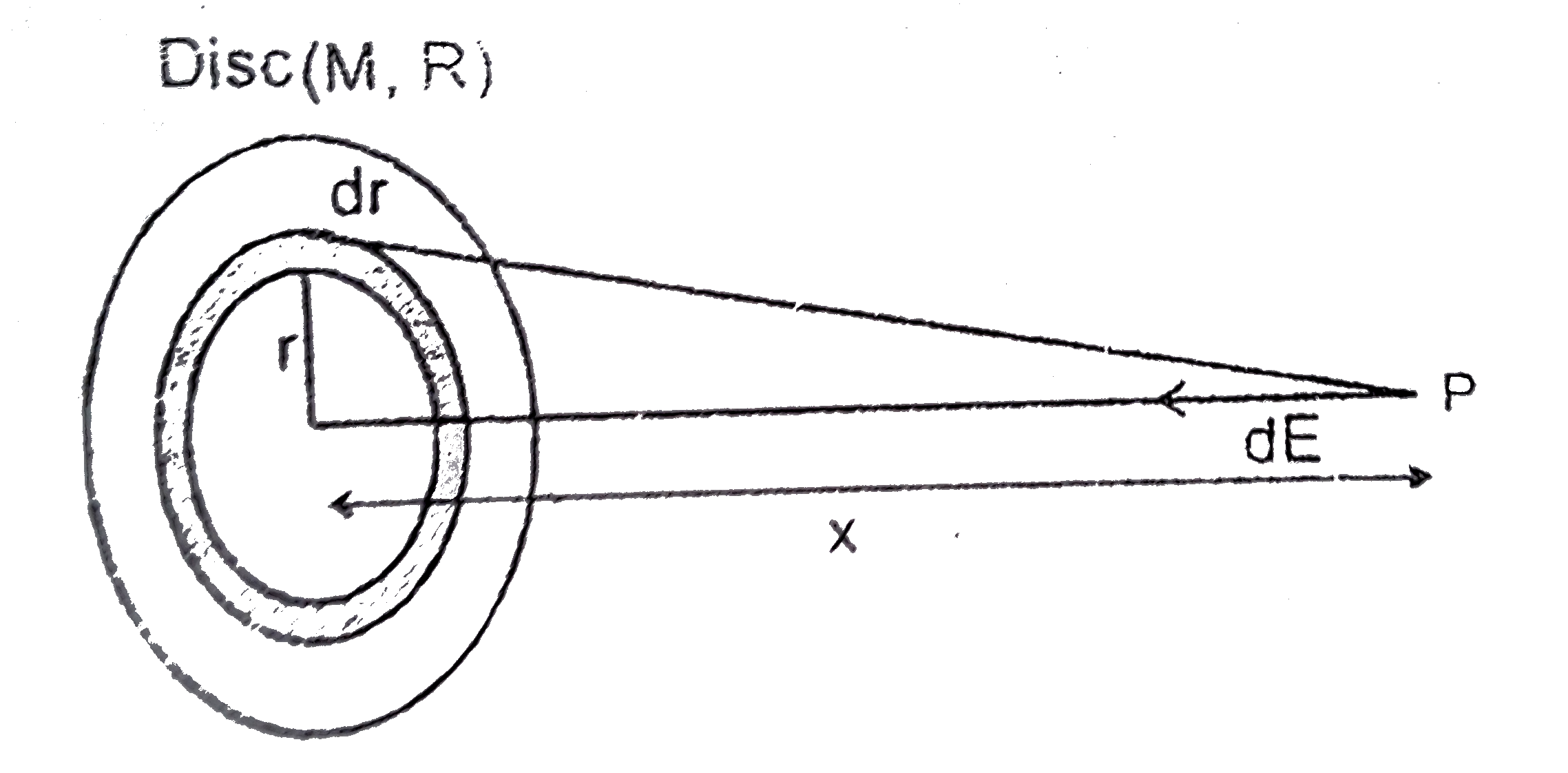
Gravitational field due to elemental ring
dE=GdMx(x2+r2)3/2 Here dM=MπR2.2πrdr=2MR2rdr
∴dE=G.2MxrdxR2(x2+r2)3/2
∴E=R∫0(2GMxR2)rdr(x2+r2)3/2
∴E=2GMxR2[1x−1√x2+R2]
Topper's Solved these Questions
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:SOLVED MISCELLANEOUS PROBLEMS
Explore 5 Videos
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:EXAMPLE
Explore 2 Videos
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Advance level Problems
Explore 35 Videos
- NUCLEAR PHYSICSBook:RESONANCEChapter:NUCLEAR PHYSICSExercise:Advanced level solutions
Explore 16 Videos
Similar Questions
Find potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionCalculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)

View Solution
Knowledge Check
The magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M and F1 and F2 respectively. Then,
AF1F2=r1r2ifr1<R and r2<RBF1F2=r21r22ifr1>R and r2>RCBoth (a) and (b)DNone of the aboveThe magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M and F1 and F2 respectively. Then,
AF1F2=r1r2ifr1<R and r2<RBF1F2=r21r22ifr1>R and r2>RCBoth (a) and (b)DNone of the aboveThe magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
AE1E2=r1r2 if r1<R and r2<RBE1E2=r22r21 if r1<R and r2<RCE1E2=r22r32 if r1<R and r2<RDE1E2=r21r22 if r1<R and r2<R
Calculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionThe magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then:
View SolutionThe magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
View SolutionThe magnitudes of the gravitational field at distance r1andr2 from the centre of a uniform sphere of radius R and mass M are F1andF2 respectively. Then :
View Solution