A 6.00m segment of a long string has a mass of 180g. A high-speed photograph shows that the segment contlains four complete cycles of a wave. The string is vibrating sinusoidally with a frequency of 50.0Hz and a peak - to - valley dispalcement of 15.0cm. (The "peak-to-valley" displacment is the vertical distance from the furthest positive displacement to the farther negative displacement.) (a) Write the funcation that describe this wave traveling in the positive x direction. (b) Determine the average power being supplied to the string.
The correct Answer is:(a) y=(7.50cm)sin(4π3×−314t+ϕ)
(b) 2025π232=625W
(a) f=500Hz
μ=180×10−36=3×10−2Kg/m
2A=15×10−2m
A=7.5×10−2m
4λ=6,λ=3/2m. and v=fλ=75m/sec
ω=2πf=100π also K=ωv=4π3
If phase constant is ϕ then
∴ equation is y=7.5×10−2sin[100πt−4π3x+ϕ]
(b) Pav=2π2f2A2μv=202532π2=625w
Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 1 PART II
Explore 31 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 2 PART I
Explore 21 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Board Level Exercise
Explore 27 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
- WAVE ON STRING Book:RESONANCEChapter:WAVE ON STRING Exercise:Exercise- 3 PART I
Explore 19 Videos
Similar Questions
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given by f(t)sin(tT). The wave speed is v. Write the wave equation.
View SolutionA 20cm long string, having a mass of 1.0g, is fixed at both the ends. The tension in the string is 0.5N. The string is into vibrations using an external vibrator of frequency 100Hz. Find the separation (in cm) between the successive nodes on the string.
View Solution
Knowledge Check
Wave of frequency 500 Hz has a phase velocity 360m/s. The phase difference between two displacement at a certain point at time 10−3s apart will be
Aπ4Bπ2CπD3π2The figure shows displacement time graph of a wave. The frequency of this wave is displacement (mm)
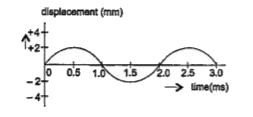 A4×10−3HzB4 HzC500 HzD1000 Hz
A4×10−3HzB4 HzC500 HzD1000 HzA string vibrates in 5 segments to a frequency of 480 Hz. The frequency that will cause it to vibrate in 2 segments will be
A96 HzB192 HzC1200 HzD2400 Hz
A 20 cm long string, having a mass of 1.0 g, is fixed at both the ends. The tension in the string is 0.5 N. The string is set into vibrations using an external vibrator of frequency 100 Hz. Find the separation (in cm) between the successive nodes on the string.
View SolutionA string of length 50cm is vibrating with a fundamental frequency of 400Hz in horizontal position. In the fundamental mode the maximum displacement at the middle is 2cm from equilibrium position and the tension in the string is 10N. Determine the maximum value of the vertical component of force on the end supporting.
View SolutionA string of length 50cm is vibrating with a fundamental frequency of 400Hz in horizontal position. In the fundamental mode the maximum displacement at the middle is 2cm from equilibrium position and the tension in the string is 10N. Determine the maximum value of the vertical component of force on the end supporting.
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA taut string from which μ=5.0×10−2 kg/m is under tension of 80 N. How much power in watt upto one decimal point must be supplied to the string to generated sinusoidal waves at a frequency of 6.0 Hz and amplitude of 6.00 cm .
View Solution

