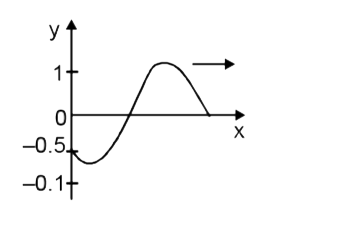
The equation of a plane wave travelling along positive direction of x-

The equation of a wave is $y = A sin (2 π n t)$ When it is reflected at a free end its amplitude becomes 90% The equation of the reflected wave is
A $y = 0.9 A sin (2 π n t + π)$
B $y = \frac{A}{9} sin (2 π n t)$
C $y = 0.9 A sin (2 π n t)$
D $y = 9 A sin (2 π n t)$
The equation of a simple harmonic progressive wave along the positive direction of X axis is given by
A $y = a sin 2 π [\frac{t}{T} - \frac{x}{λ}]$
B $y = a sin (2 π n t)$
C $y = a sin 2 π [\frac{t}{T} + \frac{x}{λ}]$
D $y = a cos (2 π n t)$
The equation of a simple harmonic progressive wave along the negative direction of X-axis is
A $y = a sin 2 π [\frac{t}{T} - \frac{x}{λ}]$
B $y = a sin (2 π n t)$
C $y = a sin 2 π [\frac{t}{T} + \frac{x}{λ}]$
D $y = a cos 2 π [x]$

The equation of a plane wave travelling along positive direction of $x -$ axis is $y = a sin \frac{2 π}{λ} (v t - x)$ When the wave is reflected at a rigid surface and its amplitude becomes $80 %$ , then find the equation of the reflected wave.