The length of the wire shown in figure between the pulleys is 1.5 m and its mass is 15 g. what is the frequency of vibration with which the wire vibrates in four loops leaving the middle point of the wire between the pullys at rest ? (g=10ms2)
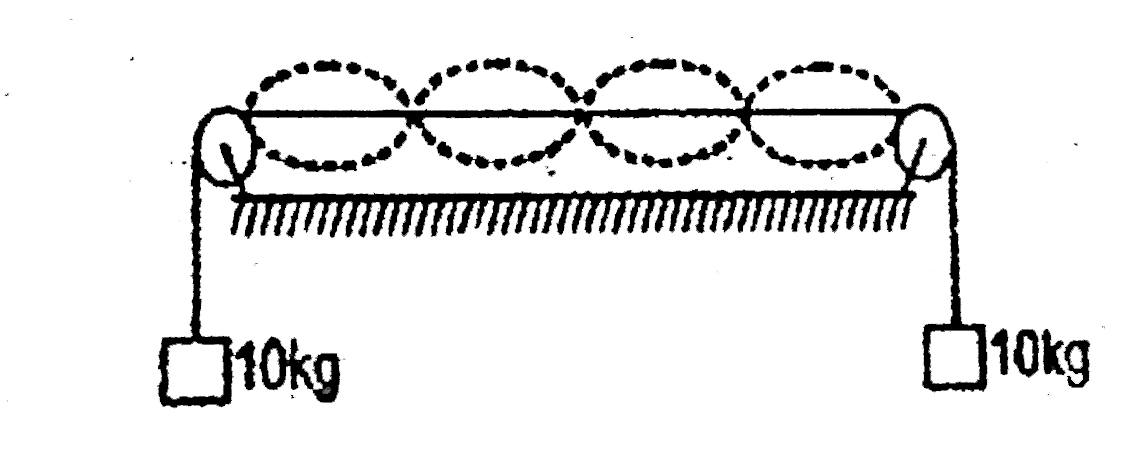
The correct Answer is:4003Hz
4λ2=1.5
λ=0.75m
v=√10×10×1.515×10−3=100m/s
f=vλ=1000.75=4003Hz.
Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 1 PART II
Explore 31 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 2 PART I
Explore 21 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Board Level Exercise
Explore 27 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
- WAVE ON STRING Book:RESONANCEChapter:WAVE ON STRING Exercise:Exercise- 3 PART I
Explore 19 Videos
Similar Questions
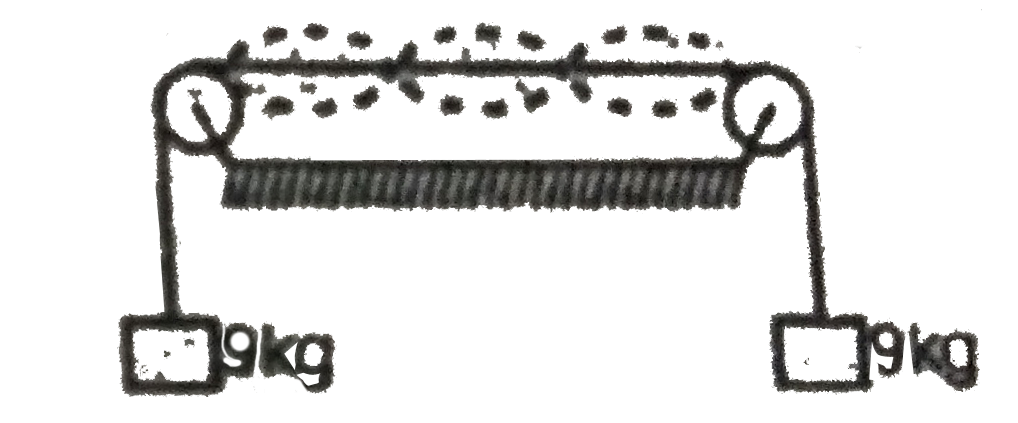
The length of the wire shown in figure between the pulley is 1.5 m and its mass is 12.0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.

View SolutionThe length of a stretched wire is 1 m and its fundamental frequency is 300 Hz.What is the speed of the transverse wave in the wire ?
View Solution
Knowledge Check
The length of the wire shown in Fig. Between the pulley and fixed support is 1.5m and mass is 12.0g the frequency of vibration with which the wire vibrate two loops leaving the middle point of the wire between the pulleys at rest isA10HzB30HzC100HzD70HzThe length of the wire shown in the figure between the pulleys is 1.5m and its mass is 12.0g. The frequency of vibration with which the wire vibrates in three loops forming antinode at the mid point of the wire is - (Take g=9.8m/s2)
 A210 HzB140 HzC70HzDnone of these
A210 HzB140 HzC70HzDnone of theseTension applied to a wire of length 1m and its mass 1g, if it is to vibrate with the fundamental frequency of 50 Hz, will be
A100NB10NC50ND2.5N
An aluminium wire of cross-sectional area (10−6)m2 is joined to a steel wire of the same cross-sectional area. This compound wire is stretched on a sonometer pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m of which the aluminium wire is 0.6m and the rest is steel wire. Transverse vibrations are setup in the wire by using an external source of variable frequency. Find the lowest frequency of excitation for which the standing waves are formed such that the joint in the wire is a node. What is the total number of nodes at this frequency? The density of aluminium is 2.6×(103)kg/m3 and that of steel is 1.04×104kg/m2(g=10m/s2)
View SolutionAn aluminimum wire of cross - sectional area 1×10−6m2 is joined to a steel wire of the same cross - sectional area . This compound wire is stretched on a sonometer , pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m of which the aluminium wire is 0.6m and the rest is steel wire . Transverse vibrations are set up in the wire by using an external source of variable frequency . Find the lowest frequency of excitation for which standing waves are formed , such that the joint in the wire is a node . What is the total number of nodes observed at this frequency , excluding the two at the ends of the wire ? The density of aluminium is 2.6×103kg/m3 and that of steel is 1.04×104kg/m3
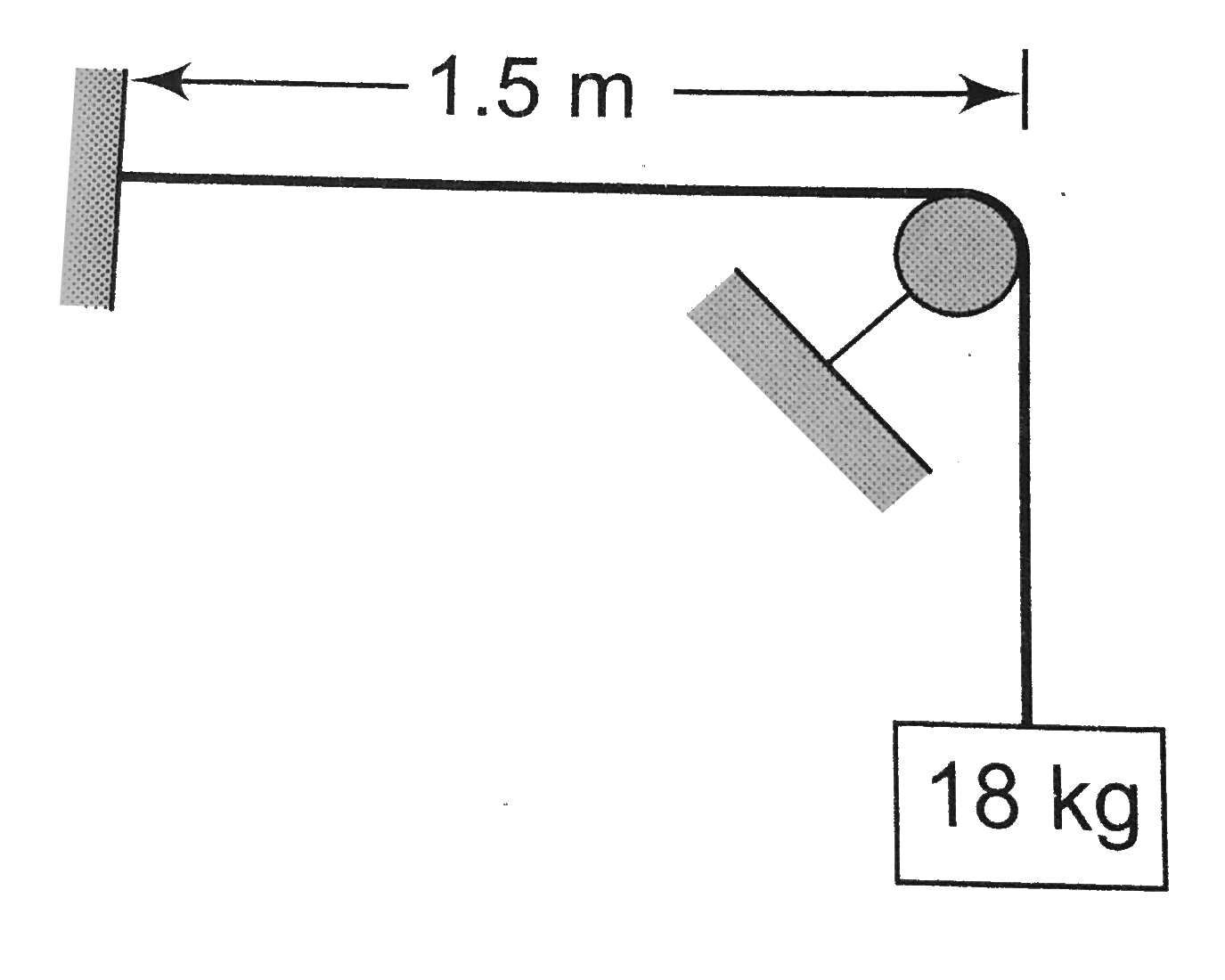
View SolutionA 50cm long wire of mass 20g supports a mass of 1.6kg as shown in figure. Find the first overtone frequency of the portion of the string between the wall and the pulley. Take g=10m/s2

View SolutionA 50 cm long wire of mass 20 g suports a mass of 1.6kg as shown in figure. Find the fundamental frequency of the portioin of the strig between the wall and the pulley. Take g=10ms−2.

View SolutionA wire is under a tension of 32N and length between the two bridges in 1m. If the length of the sample wire is 10m and its mass is 2 g, then the fundamental frequency of the wire will be
View Solution

