The streight shown in figure is driven at a frequency of . The amplitude of the motion is , and the wave speed is . Furthmore, the wave is such that and . Determine (a) the angular frequency and (b) wave number for this wave (c) Write an expression for the wave funcation. Calculate. (d) the maximum transverse speed and (e) the maximum transverse acceleration of a point on the string.
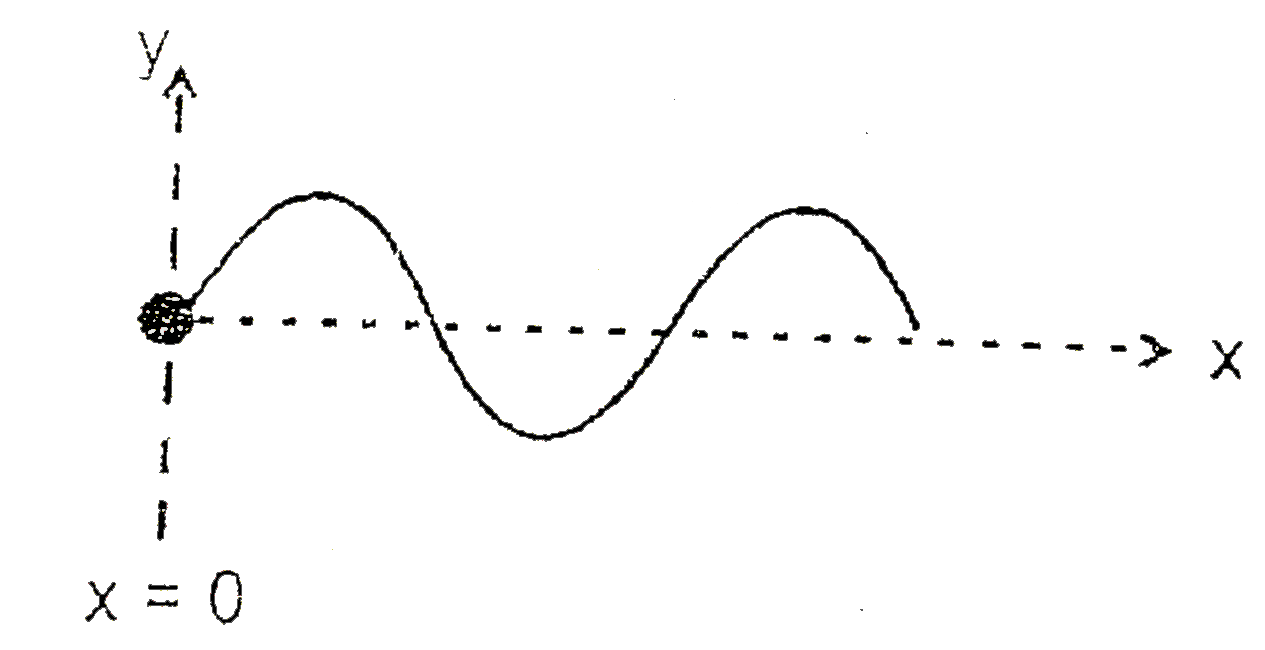
The correct Answer is:(a) , (b) , (c) , (d) (e)
(a) Red/sec
(c)
At
At
should be positive
At
should be positive
(d)
(e)
Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 1 PART II
Explore 31 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Exercise- 2 PART I
Explore 21 Videos
- TRAVELLING WAVESBook:RESONANCEChapter:TRAVELLING WAVESExercise:Board Level Exercise
Explore 27 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
- WAVE ON STRING Book:RESONANCEChapter:WAVE ON STRING Exercise:Exercise- 3 PART I
Explore 19 Videos
Similar Questions
A simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of 50.0g/m and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain.
View SolutionCalculate the wavelength, frequency, and wave number of a light wave whose period is 2.0×10−10s.
View Solution
Knowledge Check
The speed of a waves is 350 m/s and wavelength is 70 cm. The frequency of wave is :
A500 HzB700 HzC50 HzD200 HzIf the speed of a wave is 340m/s and its frequency is 1700 Hz, then λ for this wave in cm will be:
A2B0.2C20D200
Calculate the wavelength, frequency, and wave number of a light wave whose period is 2.0×10−10s.
View SolutionCalculate the wavelength, frequency, and wave number of a light wave whose period is 2.0×10−10s.
View SolutionEquation of a transverse wave travelling in a rope is given by
y=5sin(4.0t−0.02x)
where y and x are expressed in cm and time in seconds. Calculate
(a) the amplitude, frequency,velocity and wavelength of the wave.
(b) the maximum transverse speed and acceleration of a particle in the rope.
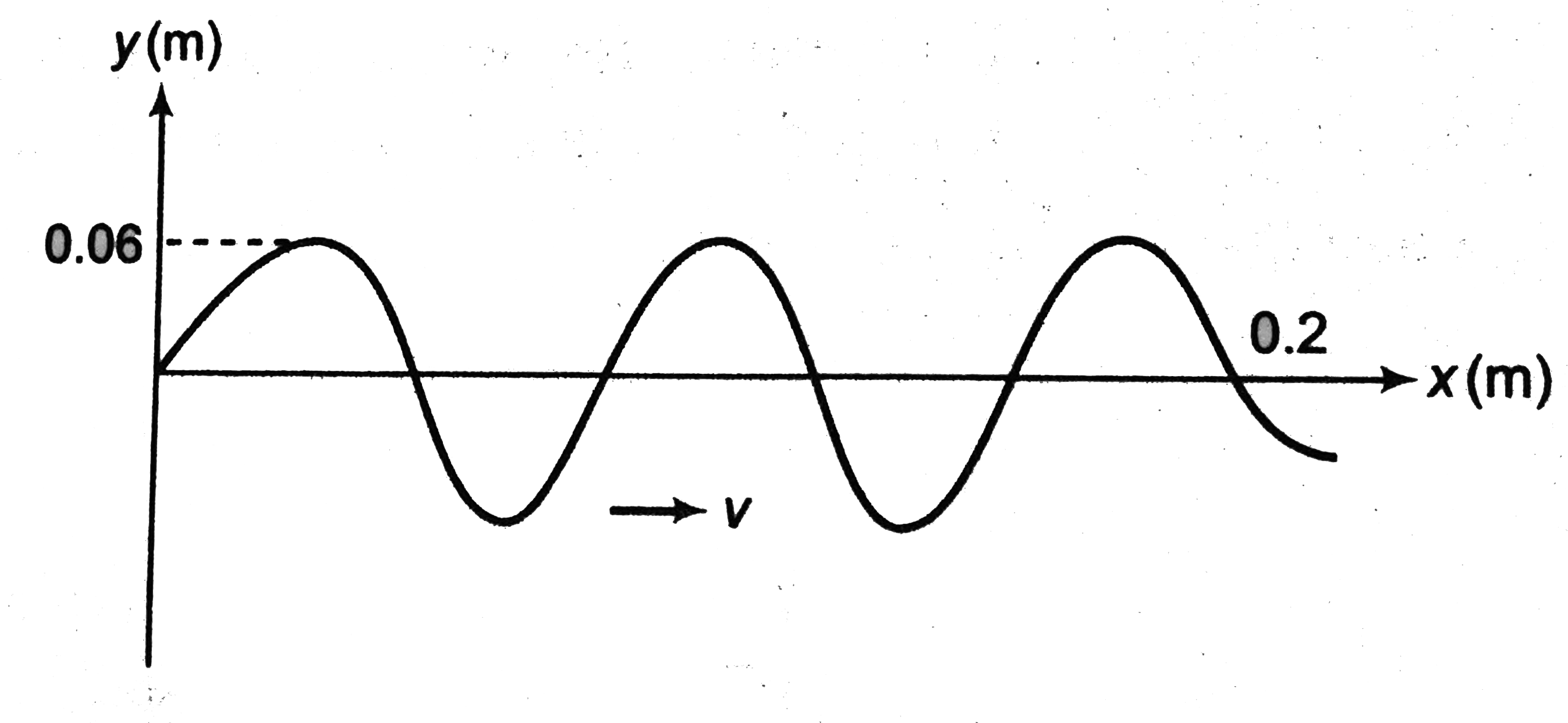
View SolutionFor the wave shown in figure, write the equation of this wave if its position is shown at t=0. Speed of wave is v=300m/s.
View SolutionA trasverse wave of amplitude 0.50mm and frequency 100Hz is produced on a wire stretched to a tension of 100N. If the wave speed is 100m/s. What average power is the source transmitting to the wire?
View SolutionA transverse wave of amplitude 0.50 mm and frequency 100 Hz is produced on a wire stretched to a tension of 100 N. If the wave speed is 100 m s^-1, what average power is the source transmitting to the wire ?
View Solution

