A spring mass system has time period of 2 second. What should be the spring constant of spring if the mass of the block is 10grams ?
The correct Answer is:0.1N/m
To solve the problem step by step, we will use the formula for the time period of a spring-mass system in simple harmonic motion.
Step 1: Write down the formula for the time period
The time period T of a spring-mass system is given by the formula:
T=2π√mk
where:
- T is the time period,
- m is the mass of the block,
- k is the spring constant.
Step 2: Rearrange the formula to solve for k
To find the spring constant k, we can rearrange the formula:
k=4π2mT2
Step 3: Convert the mass into kilograms
The mass is given as 10 grams. We need to convert this into kilograms:
m=10 grams=0.01 kg
Step 4: Substitute the values into the formula
Now we can substitute the values of m and T into the rearranged formula. We know T=2 seconds:
k=4π2(0.01)(2)2
Step 5: Calculate k
Now we will calculate k:
k=4π2(0.01)4
k=π2(0.01)
Using the approximate value of π≈3.14:
k≈(3.14)2×0.01
k≈9.86×0.01
k≈0.0986 N/m
Step 6: Round off the answer
Rounding off 0.0986 N/m gives us:
k≈0.1 N/m
Thus, the spring constant k is approximately 0.1 N/m.
Final Answer:
The spring constant of the spring should be 0.1 N/m.
---
The time period T of a spring-mass system is given by the formula:
T=2π√mk
where:
- T is the time period,
- m is the mass of the block,
- k is the spring constant.
To find the spring constant k, we can rearrange the formula:
k=4π2mT2
The mass is given as 10 grams. We need to convert this into kilograms:
m=10 grams=0.01 kg
Now we can substitute the values of m and T into the rearranged formula. We know T=2 seconds:
k=4π2(0.01)(2)2
Now we will calculate k:
k=4π2(0.01)4
k=π2(0.01)
Using the approximate value of π≈3.14:
k≈(3.14)2×0.01
k≈9.86×0.01
k≈0.0986 N/m
Rounding off 0.0986 N/m gives us:
k≈0.1 N/m
The spring constant of the spring should be 0.1 N/m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - II
Explore 37 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - I
Explore 26 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Board Level Exercise
Explore 24 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
Knowledge Check
A block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
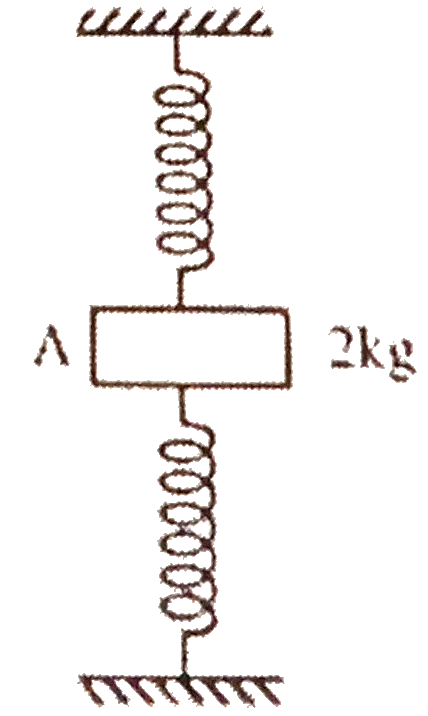 A6.5m/s2B7.5m/s2C10m/s2D8m/s2
A6.5m/s2B7.5m/s2C10m/s2D8m/s2The time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
A0.2πsB0.21πsC0.22πsD0.02πsTime period of a spring mass system can be changed by
Achanging the massBacclerating the point of suspension of the blockCcutting the spring (i.e.changing the length of the spring)Dimmersing the mass in a liquid
Find the time period of the oscilltion of mass m in figure a and b. What is the equivalent spring constant of the spring in each case. ?

View SolutionA spring-block system is executing SHM. The mass of the block is M and the time period of oscillation is T. If the mass of the block is increased by m, then time period becomes 7T4. Now, find the ratio of mM ,
View SolutionA mass is suspended at the end of a spring and performs SHM with a time period 3 seconds, while the time period f same mass with other spring is 4 second. If that mass is connected with the combination of the two springs connected in series then time period of oscillator is
View SolutionA block with a mass of 3.00kg is suspended from an ideal spring having negligible mass and stretches the spring by 0.2m.
(a) What is the force constant of the spring?
(b) What is the period of oscillation of the block if it is pulled down and released ?
View SolutionA block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be

View Solution

