Instantaneous angle (in radian) between string of a simple pendulum and verical is given by $θ = \frac{π}{180} sin 2 π t$ . Find the length of the pendulum if $g = π^{2} m / s^{2}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $0.25 m$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Instantaneous angle (in radian) between string of a simple pendulum and verical is given by theta = (pi)/(180) sin2pit. Find the length of the pendulum if g = pi^(2) m//s^(2). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Knowledge Check

The period of a simple pendulum is double, when its length is increased by 1.2 m. The original length of the simple pendulum is
A0.2 m
B0.3 m
C0.4 m
D0.5 m
A simple pendulum is oscillating at $\frac{3}{4} t h$ of a second, where g = 980 cm ${sec}^{2}$ , the length of the pendulum is
A55.85 cm
B48.5 cm
C13.96 cm
D42.2 cm
The instantaneous displacement of a simple pendulum oscillator is given by $x = A cos (ω t + \frac{π}{4})$ Its speed will be maximum at time
A $\frac{π}{4 ω}$
B $\frac{π}{2 ω}$
C $\frac{π}{ω}$
D $\frac{2 π}{ω}$

RESONANCE-SIMPLE HARMONIC MOTION -Exercise- 1, PART - I

Home
Ask Doubt
Profile

Instantaneous angle (in radian) between string of a simple pendulum and verical is given by θ=π180sin2πt. Find the length of the pendulum if g=π2m/s2.

The correct Answer is:0.25m

Topper's Solved these Questions

Similar Questions

Knowledge Check

The period of a simple pendulum is double, when its length is increased by 1.2 m. The original length of the simple pendulum is

A simple pendulum is oscillating at 34th of a second, where g = 980 cm sec2, the length of the pendulum is

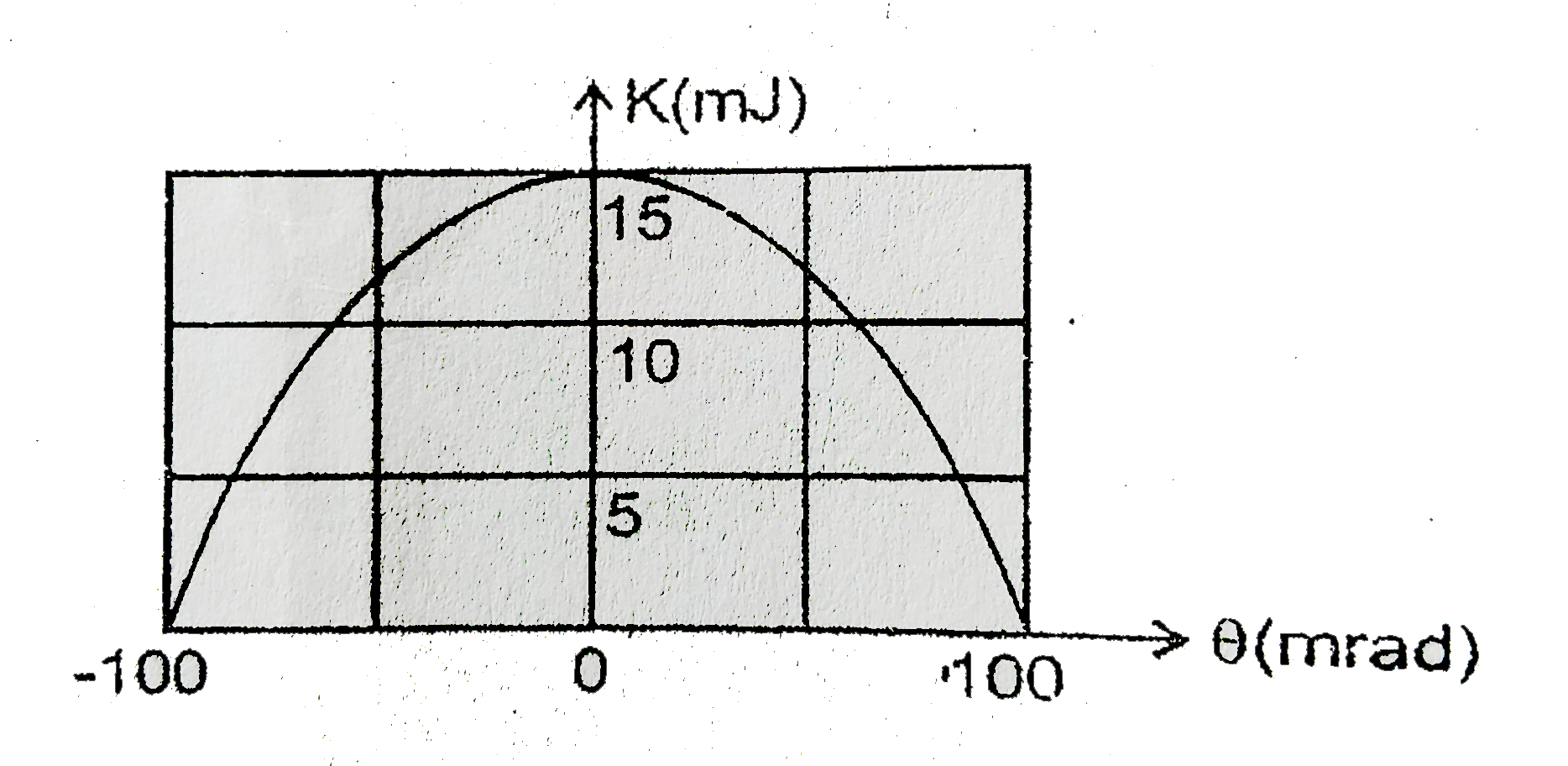
The instantaneous displacement of a simple pendulum oscillator is given by x=Acos(ωt+π4)Its speed will be maximum at time

RESONANCE-SIMPLE HARMONIC MOTION -Exercise- 1, PART - I

Instantaneous angle (in radian) between string of a simple pendulum and verical is given by $θ = \frac{π}{180} sin 2 π t$ . Find the length of the pendulum if $g = π^{2} m / s^{2}$ .

The correct Answer is: $0.25 m$

A simple pendulum is oscillating at $\frac{3}{4} t h$ of a second, where g = 980 cm ${sec}^{2}$ , the length of the pendulum is

The instantaneous displacement of a simple pendulum oscillator is given by $x = A cos (ω t + \frac{π}{4})$ Its speed will be maximum at time