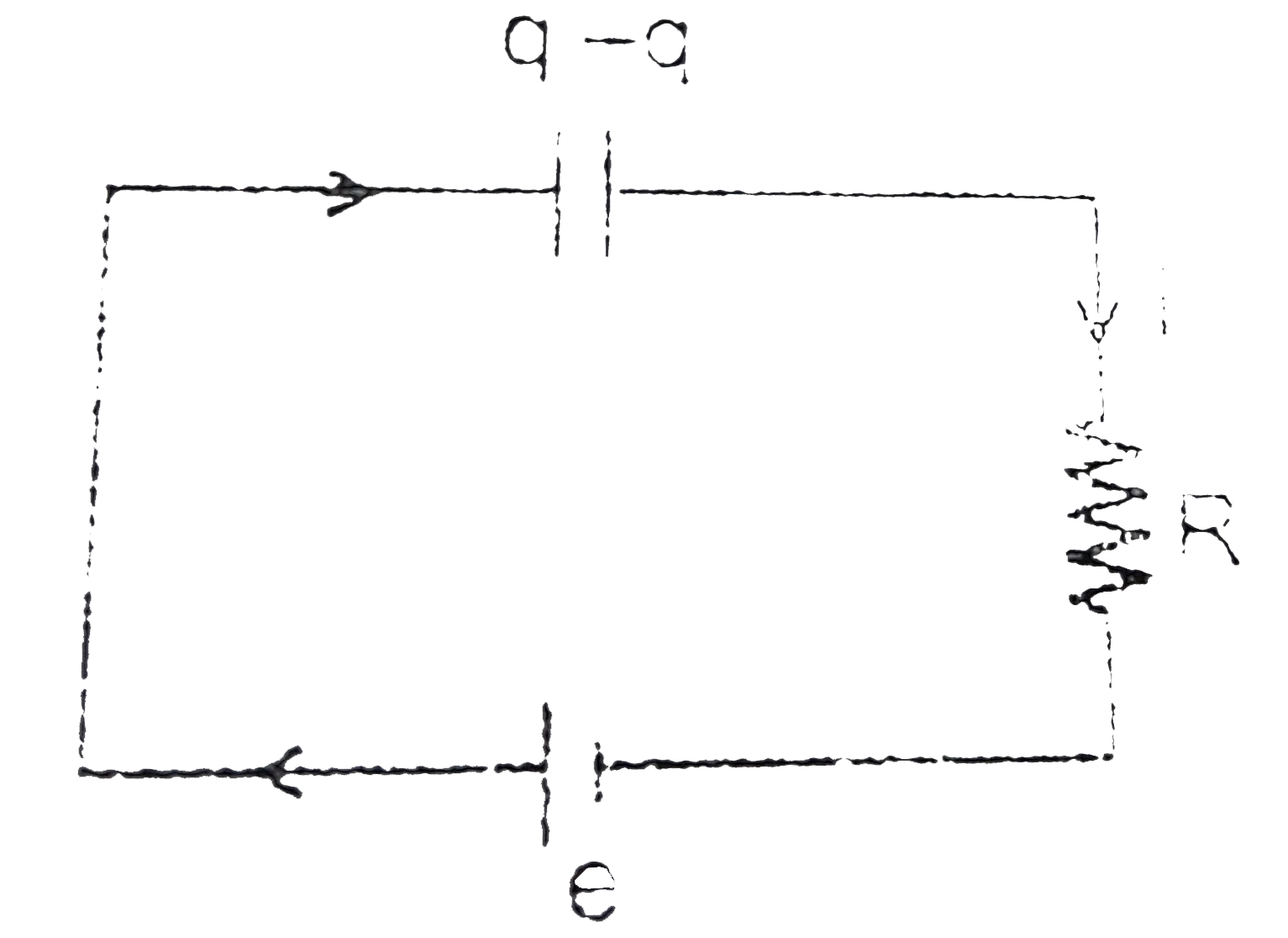
If the current in the ineer loop changes according to i=2t2 then, find the current in the capacitor as a function of time.

M=μ02bπa2
|emf induced in larger coil|=M[(didt)in smaller coil]
e=μ02bpa2(4t)=2μ0πa2tb
Applying KVL:-
+e−qc−iR=0
2μ0πa2tb−qc=iR=0
differentiate wrt time :-
2μ0πa2tb−ic−didtR=0
on solving it
i=2μ0πa2tb[1−e−t/RC]
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Problem
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-1
Explore 63 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:HLP
Explore 39 Videos
Similar Questions
If the current in the inner loop changes according to I=2t2 (Fig .), then find the current in the capacitor as a function of time.

View SolutionFind the current in the loop
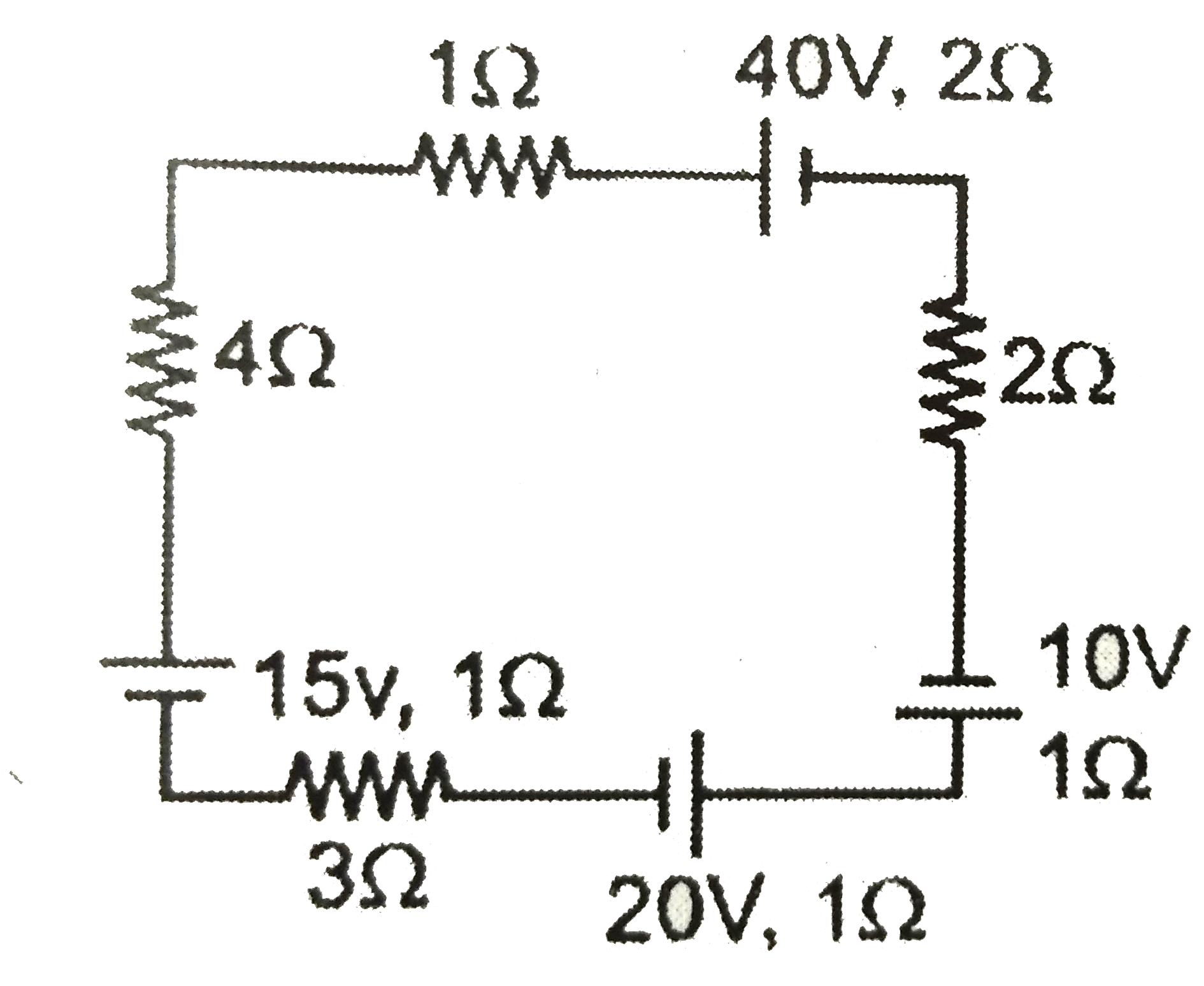
View SolutionFind the current in the loop.
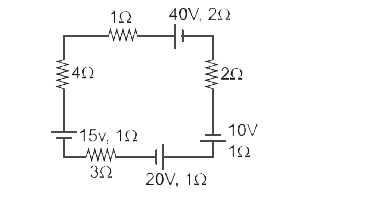
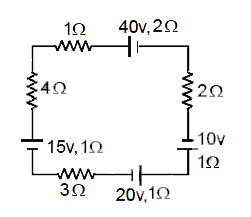
View SolutionFind the current in the loop.
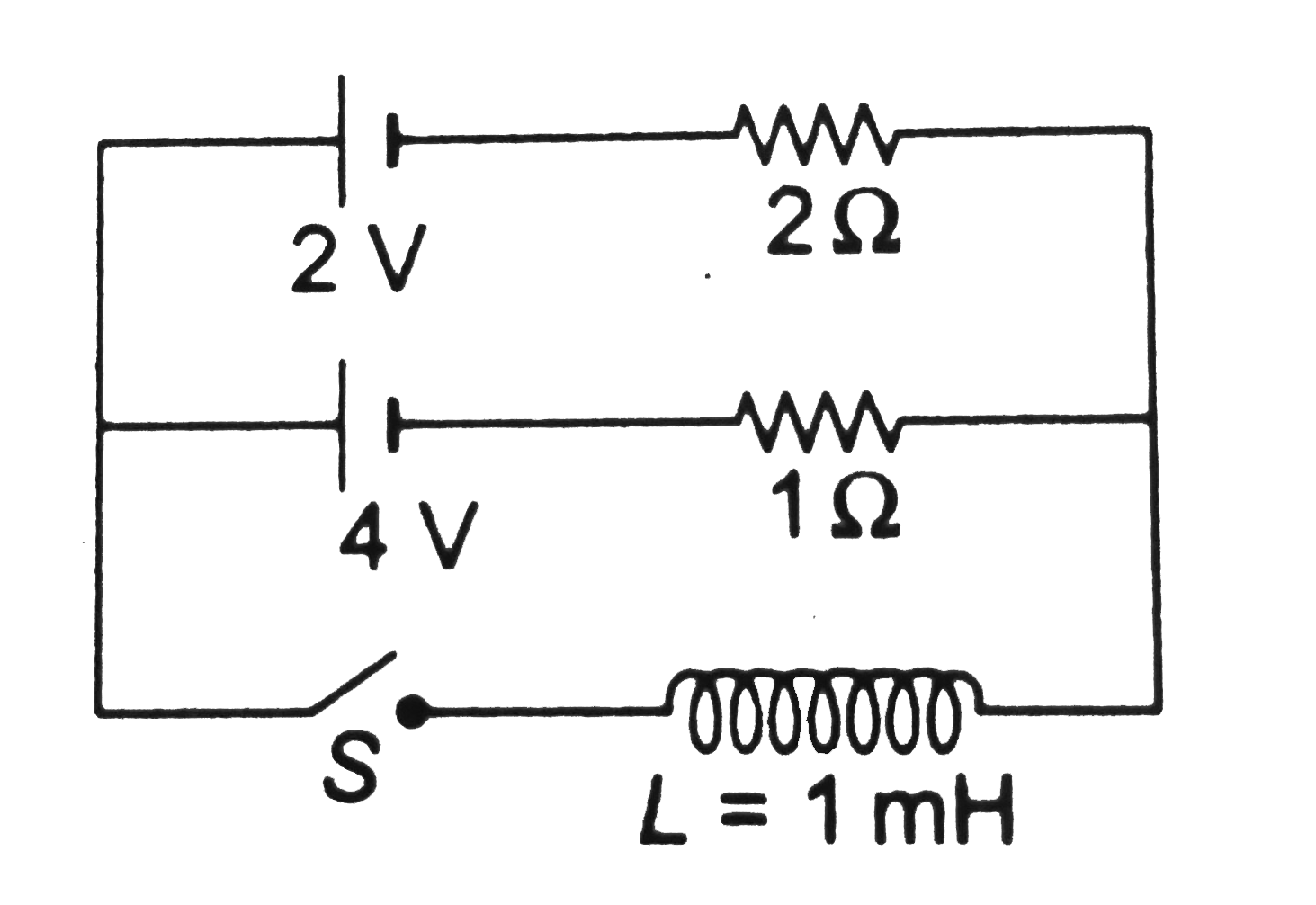
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
View SolutionFigure. shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop,
a. find the mutual inductance of the two coils,
b. find the emf induced in the larger coil,
c. if the resistance of the larger loop is R, find the current in it as a function of time.

View SolutionFigure shows tow concentric coplanar coils with radii a and b (a<<b). A current i=2t flows in the smaller loop. Neglecting self inductance of larger loop

(a) Find the mutual inductance of two coils.
(b) Find the emf induced in the larger coil
(c) If the resistance of the larger loop is R find the current in it as a function of time.
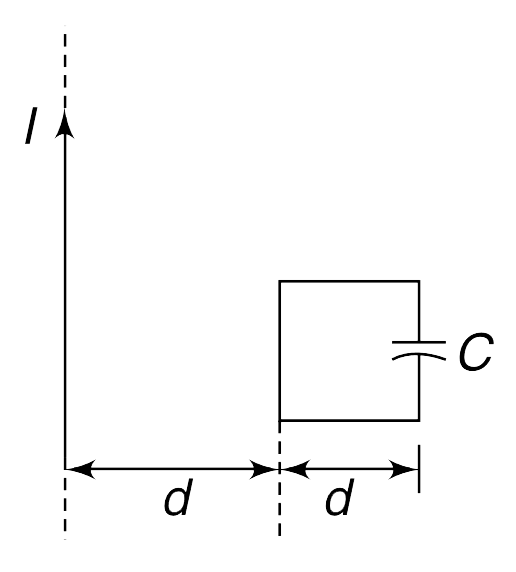
View SolutionA square loop of side length d has a capacitor of capacitance C and the resistance of the loop is R. In the plane of the loop there is a long straight current carrying wire having current I. The distance of the straight wire from the loop is d as shown in figure. The current in the straight wire is made to grow with time as I=αt where α=2As−1. Neglect self inductance of the loop.
(a) Find the charge on the capacitor as a function of time (t).
(b) Find the heat generated in the loop as a function of time.
(c) Who supplies energy for heat dissipation?
View SolutionIn Fig. 30-44, after switch S is closed at time t = 0, the emf of the source is automatically adjusted to maintain a constant current i through S. (a) Find the current through the inductor as a function of time. (b) At what time is the current through the resistor equal to the current through the inductor?

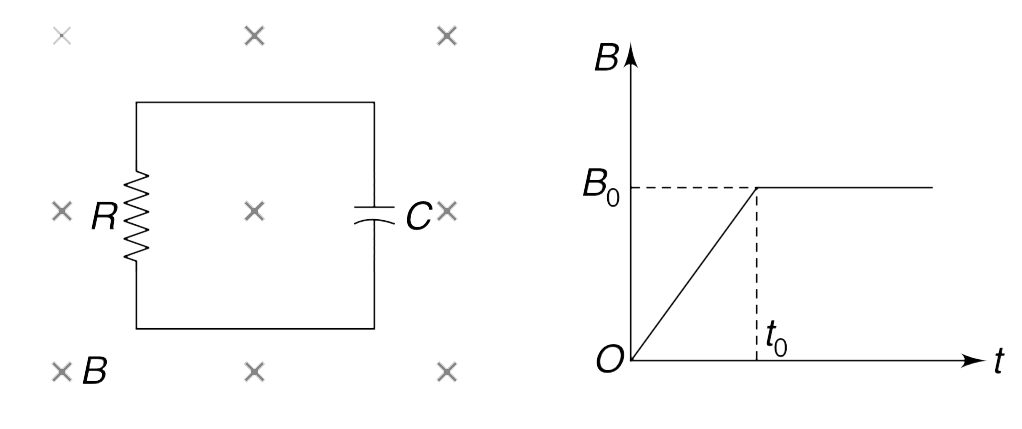
View SolutionA conducting loop having resistance R contains a capacitor of capacitance C. A uniform magnetic field B is applied perpendicular to the plane of the loop. The magnetic field is made to change with time as depicted in the graph [t0=2RC]. Plot the variation of charge on the capacitor as a function of time (t).
View Solution