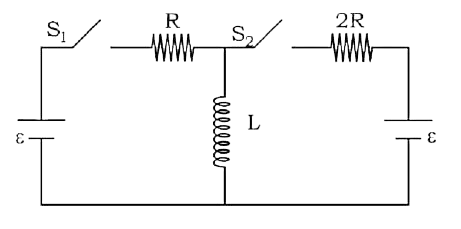
In a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

Before S2 is closed and S1 is opened current in the left part of the circuit =εR
Now when S2 closed S1 opened current through the inductor can not charge suddenly current εR will continue to move in the inductor.
Applying KVL in loop 1. ?
Ldidt+εR(2R)=4ε=0
didt=−6εL
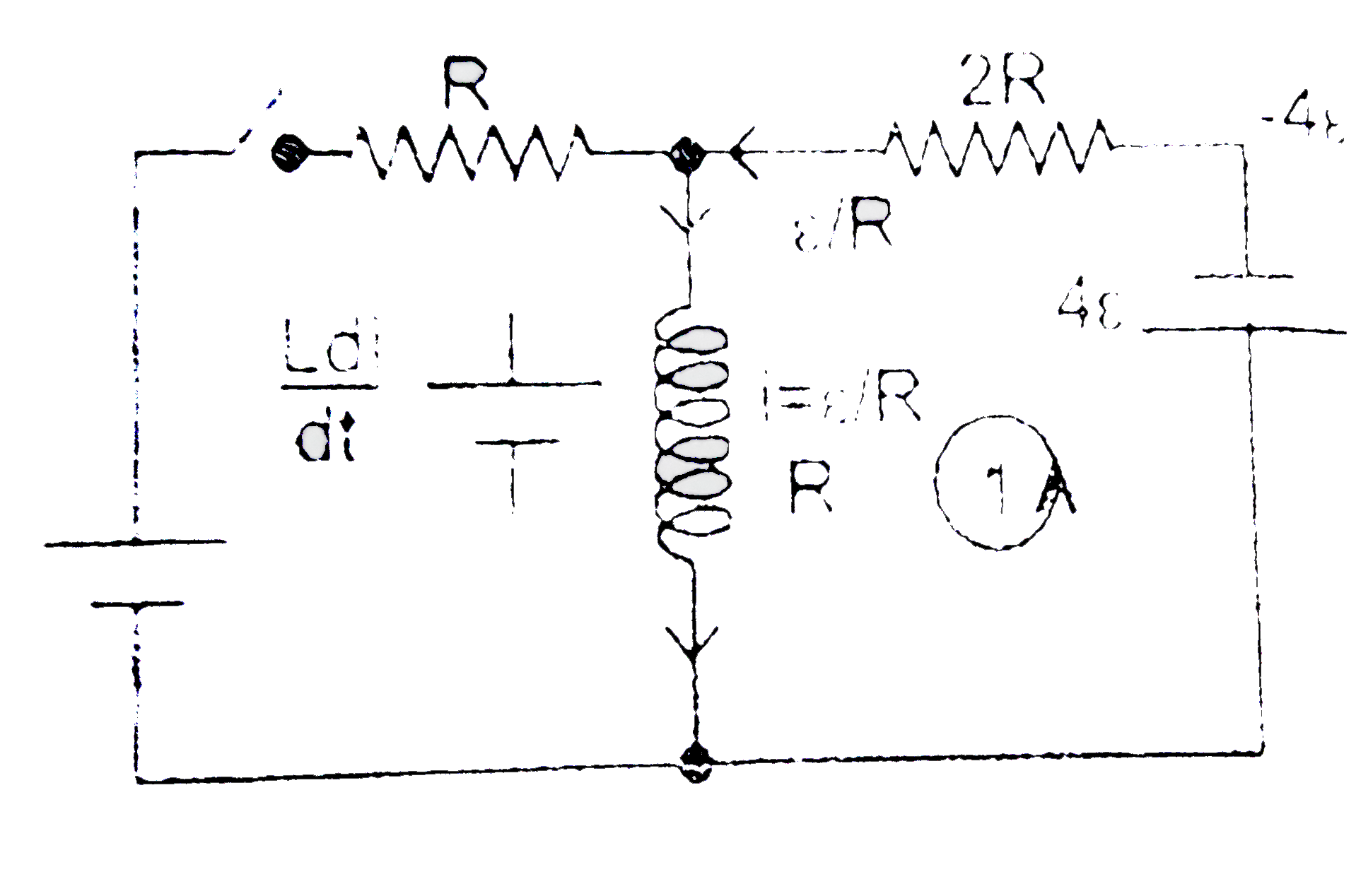
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem12videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-163videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems31videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - HLP39videos
ELECTROSTATICS
Similar Questions
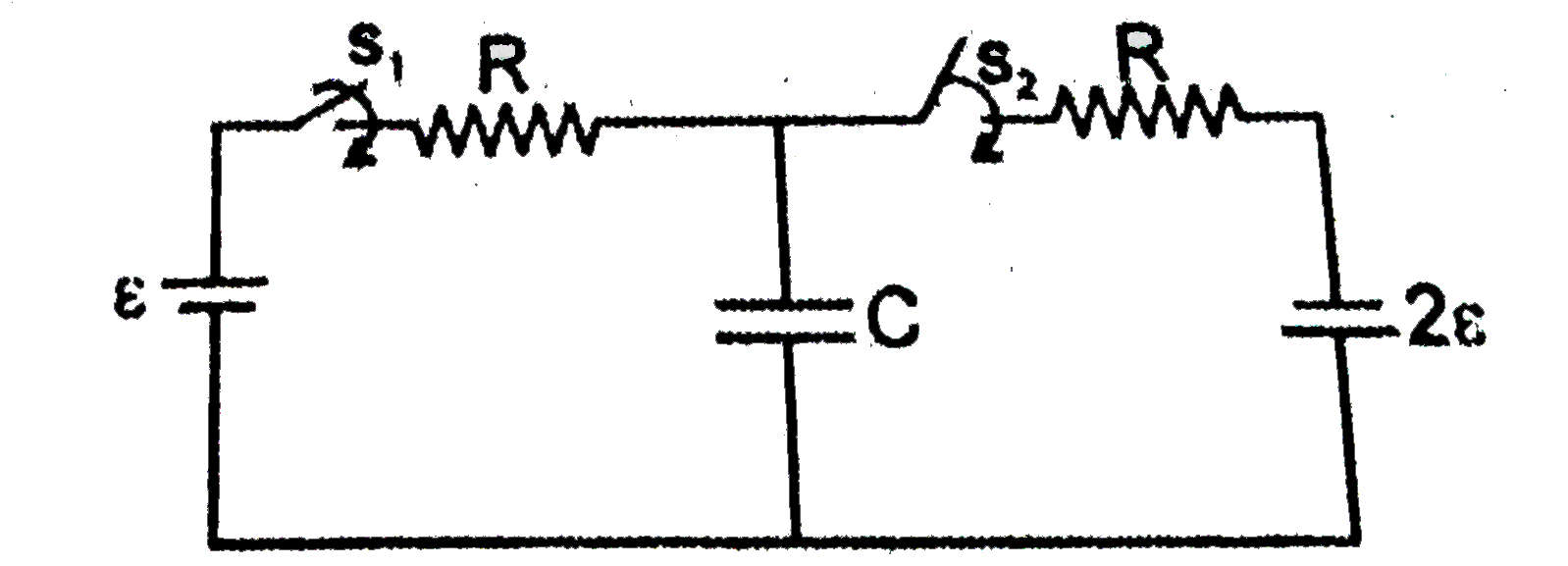
At t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out

Charge on the capacitor long after that moment.View SolutionAt t=0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
(i) The current through the capacitor immediately after that moment
(ii) Charge on the capacitor long after that moment.
(iii) Total charge flown through the cell of emf 2ε after S2 is closed.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
The capacitor 'C' is initially unchanged. Switch S1 is closed for a long time while S2 remains open. Now at t=0S2 is closed while S1 is opened. All the batteries are ideal and connecting wires are resistanceless
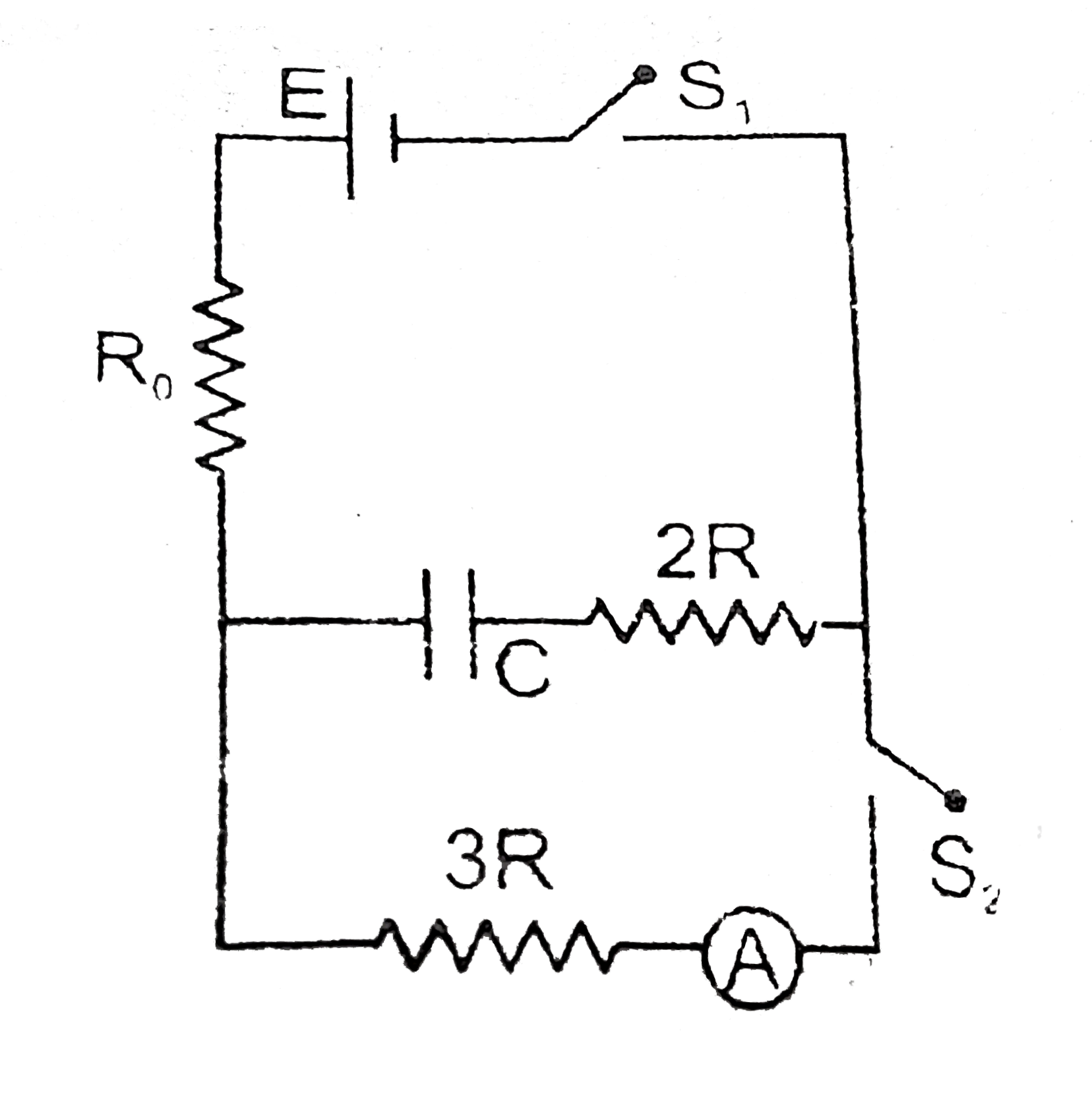 AAt time t = 0, reading of ammeter is E5RBAt time t =0, reading of ammeter is zeroCHeat developed till time t=5RCln2 in resistance 3 R is 940CE2DAfter time t>0 charge on the capacitor follows the equation CEe−t/5RC
AAt time t = 0, reading of ammeter is E5RBAt time t =0, reading of ammeter is zeroCHeat developed till time t=5RCln2 in resistance 3 R is 940CE2DAfter time t>0 charge on the capacitor follows the equation CEe−t/5RC - Question 2 - Select One or More
As shown in diagram initial charge on capacitor is zreo . Now switch S1 is closed & it remains closed for a long time but S2 remains open . Now switch S1 is opened & switch S2 is closed at t=0, then after closing the switch S2 :
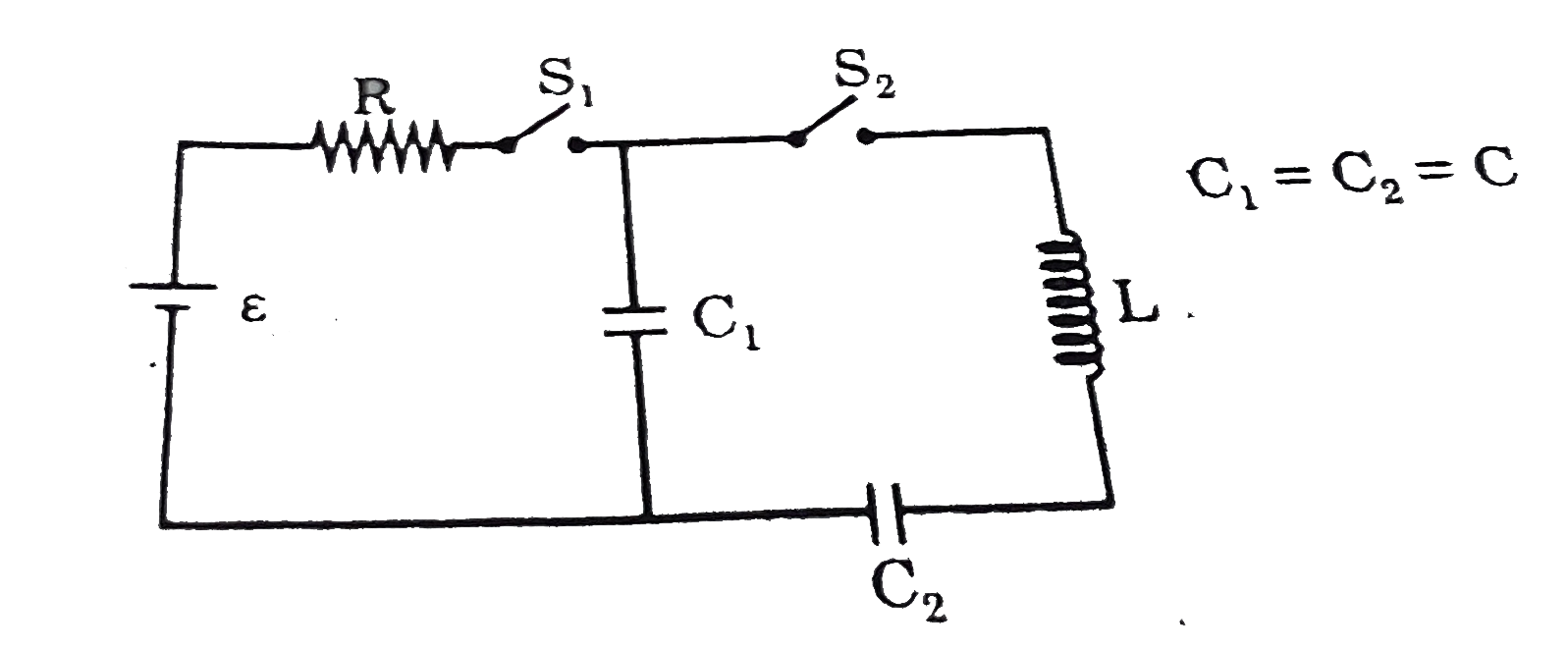 AMaximum current passing through inductor will be (ε)√C2L.BMaximum magnitude of rate of change of current through inductor will be εL.CMaximum charge on capacitor C2 will be εC.DMaximum charge on capacitor C2 will be εC2.
AMaximum current passing through inductor will be (ε)√C2L.BMaximum magnitude of rate of change of current through inductor will be εL.CMaximum charge on capacitor C2 will be εC.DMaximum charge on capacitor C2 will be εC2. - Question 3 - Select One
In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
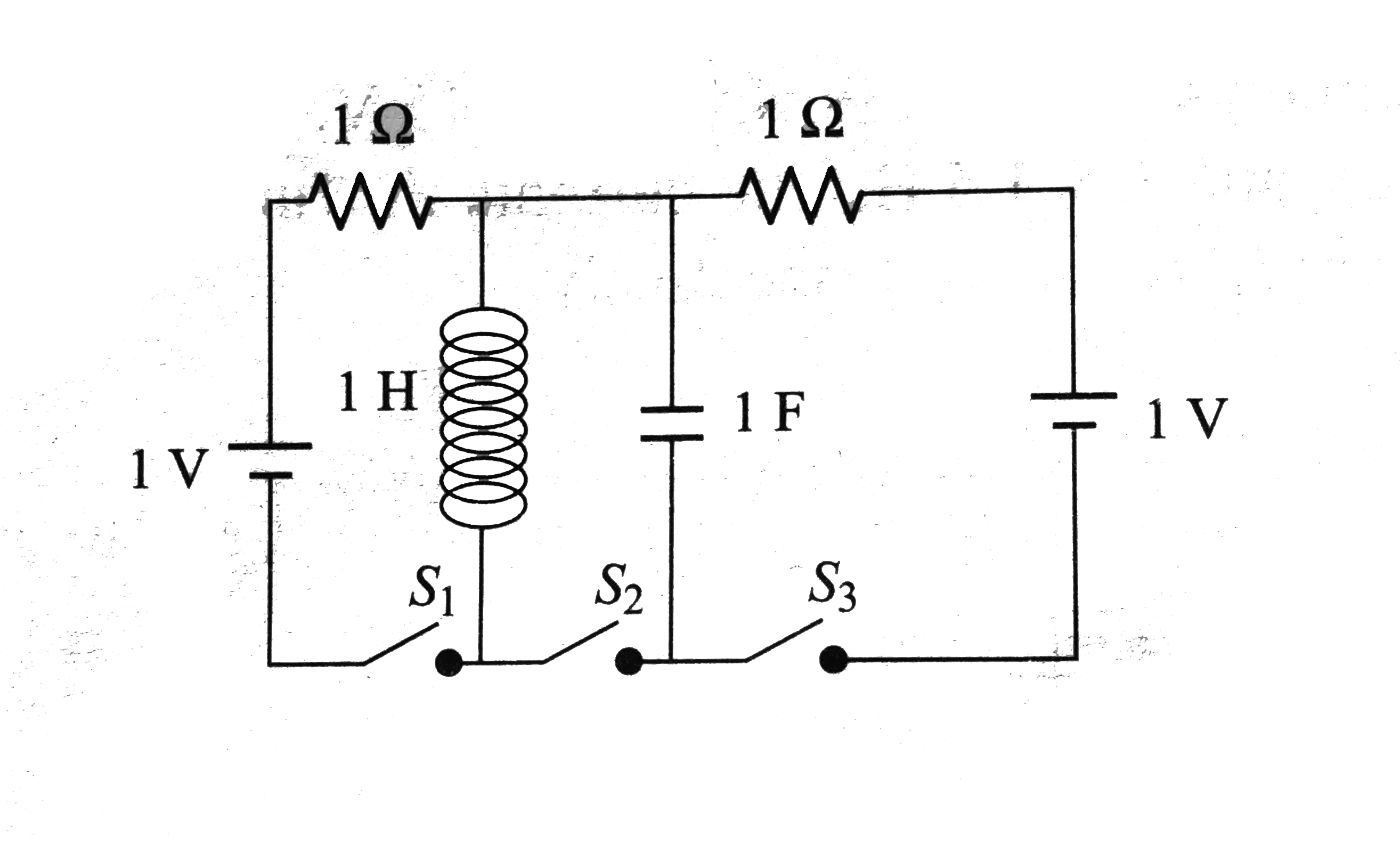
the maximum current in the circuit containing inductor and capacitor (only S2 is closed)A√3(1−1e)B√2(1−1e)C√3(1+1e)D√2(1+1e)
At t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
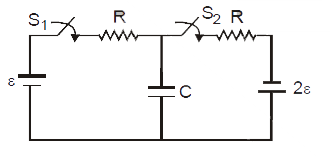
The current through the capacitor immediately after that momentView SolutionAt t =0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
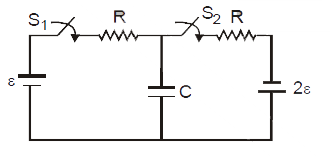
Total charge flown through the cell of emf 2ε after S2 is closed.View SolutionIn the circuits shows in S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, find the potential difference (V) across R and di/dt (with sign) in L.
 View Solution
View SolutionInitally switch S1 is closed, after a long time, S1 is opened and S2 is closed. Find the heat produced in coil after long time.
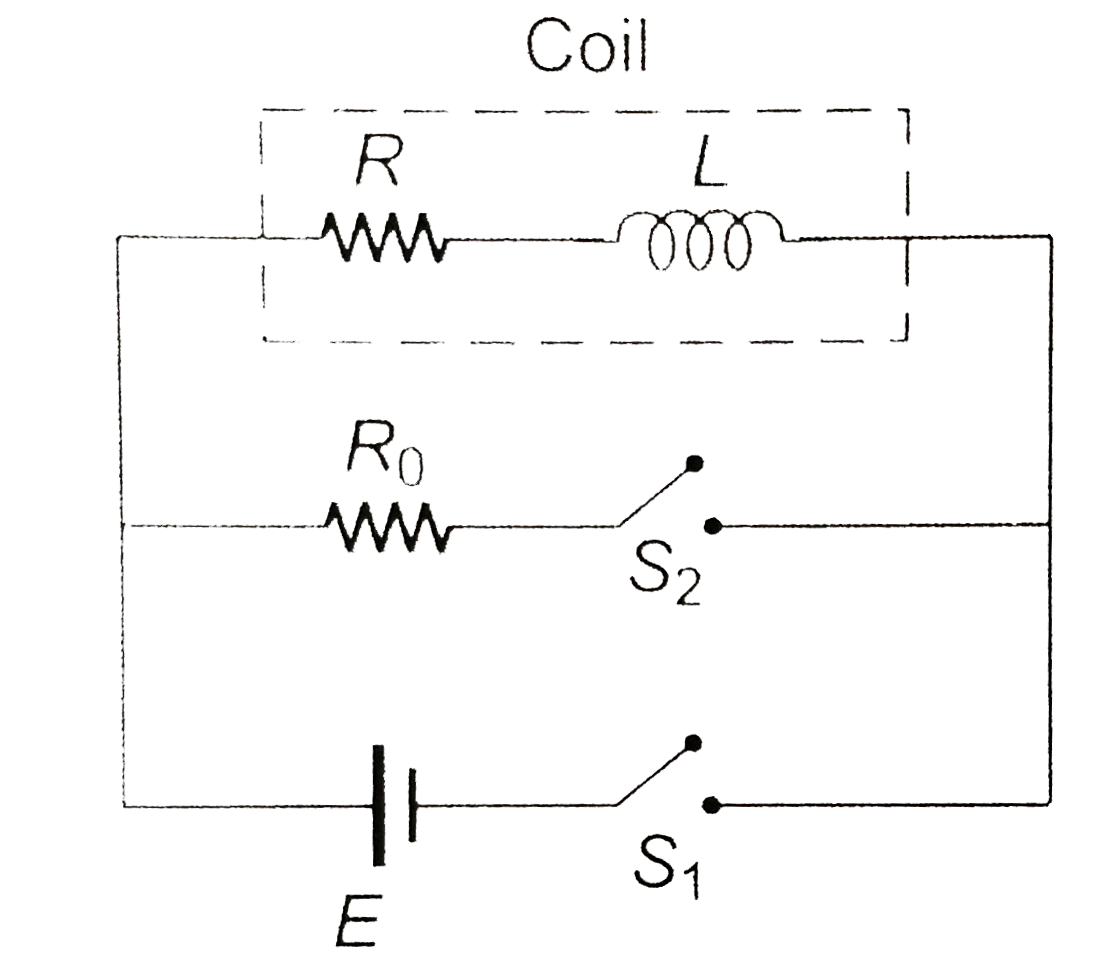 View Solution
View SolutionIn the given circuit S1 and S2
are switches. S2 is closed for
a long time and S1 remains
Open. Now S1 is also closed. Here
R=10Ω,L=1 mH and
ε=3V.Letdidt is the
magnitude of rate of change of
current (in"A/s"). Just after S1
is Closed. The value for the
inductor L is
didt=x×103A/s. Then find x.
 View Solution
View Solution

